题目内容
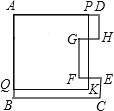
【题目】 如图,在边长为4的正方形纸片ABCD中,从边CD上剪去一个矩形EFGH,且有EF=DH=CE=1cm,FG=2cm,动点P从点A开始沿AD边向点D以1cm/s的速度运动至点D停止.以AP为边在AP的下方做正方形AQKP,设点P运动时间为t(s),正方形AQKP和纸片重叠部分的面积为S(cm2),则S与t之间的函数关系用图象表示大致是( )
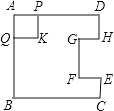
A. 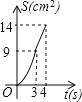 B.
B. 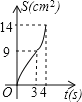
C. 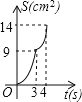 D.
D. 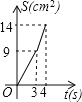
【答案】C
【解析】
分①0≤t≤3时,重叠部分为边长为AP的正方形,②3<t≤4时,重叠部分为正方形APKQ的面积减去一个矩形的面积,然后列式整理得到S与t的关系式,再根据各选项图象判断即可.
解:
∵EF=DH=CE=1cm,FG=2cm,
∴GF到AB的距离为3,
①0≤t≤3时,重叠部分为边长为AP的正方形,
此时,S=t2;
②3<t≤4时,S=t2-2(t-3)=t2-2t+6,
纵观各选项,只有C选项图象符合.
故选:C.

练习册系列答案
相关题目