题目内容
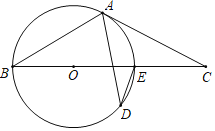
【题目】如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C，
(1)若∠ADE＝28°，求∠C的度数；
(2)若AC＝6，CE＝3，求⊙O半径的长．
【答案】(1)∠C＝34°；(2)⊙O半径的长是
．
【解析】
(1)连接OA，根据圆周角定理求出∠AOC，根据切线的性质求出∠OAC，根据三角形内角和定理求出即可；
(2)设OA＝OE＝r，根据勾股定理得出方程，求出方程的解即可．
解：(1)如图，连接OA，
∵∠ADE＝28°，
∴由圆周角定理得：∠AOC＝2∠ADE＝56°，
∵AC切⊙O于A，
∴∠OAC＝90°，
∴∠C＝180°﹣∠AOC﹣∠OAC＝180°﹣56°﹣90°＝34°；
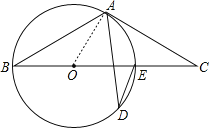
(2)设OA＝OE＝r，
在Rt△OAC中，由勾股定理得：OA2+AC2＝OC2，
即r2+62＝(r+3)2，
解得：r＝，
答：⊙O半径的长是．
练习册系列答案
金钥匙试卷系列答案
相关题目
