题目内容
如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
| A.25°; | B.30°; | C.45°; | D.60°. |
B
解析试题分析:先根据图形折叠的性质得出BC=CE,再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE,进而可判断出△BEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论.
∵△ABC沿CD折叠B与E重合,
∴BC=CE,
∵E为AB中点,△ABC是直角三角形,
∴CE=BE=AE,
∴△BEC是等边三角形.
∴∠B=60°,
∴∠A=30°,
故选B.
考点:折叠的性质,直角三角形的性质,等边三角形的判定和性质
点评:解题的关键是熟练掌握折叠的性质:折叠前后的对应边相等,对应角相等.

练习册系列答案
相关题目
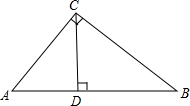 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于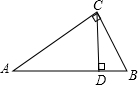 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=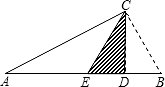 如图,CD是Rt△ABC斜边AB上的高,直角边AC=
如图,CD是Rt△ABC斜边AB上的高,直角边AC=