题目内容
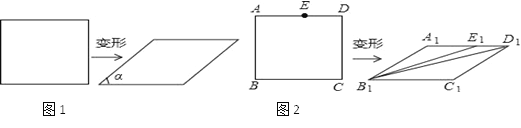
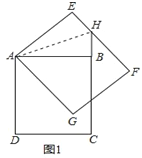
【题目】如图1,在矩形ABCD中,AD=4,AB=2![]() ,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
,将矩形ABCD绕点A逆时针旋转α(0<α<90°)得到矩形AEFG.延长CB与EF交于点H.
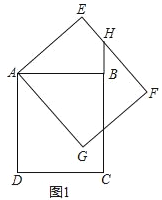
(1)求证:BH=EH;
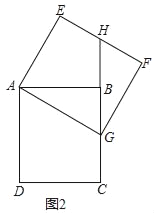
(2)如图2,当点G落在线段BC上时,求点B经过的路径长.
【答案】(1)见解析;(2)B点经过的路径长为![]() .
.
【解析】分析:(1)、连接AH,根据旋转图形的性质得出AB=AE,∠ABH=∠AEH=90°,根据AH为公共边得出Rt△ABH和Rt△AEH全等,从而得出答案;(2)、根据题意得出∠EAB的度数,然后根据弧长的计算公式得出答案.
详解:(1)、证明:如图1中,连接AH,
由旋转可得AB=AE,∠ABH=∠AEH=90°,又∵AH=AH,∴Rt△ABH≌Rt△AEH,∴BH=EH.
(2)、解:由旋转可得AG=AD=4,AE=AB,∠EAG=∠BAC=90°,在Rt△ABG中,AG=4,AB=2![]() ,
,
∴cos∠BAG=![]() ,∴∠BAG=30°,∴∠EAB=60° ,∴弧BE的长为
,∴∠BAG=30°,∴∠EAB=60° ,∴弧BE的长为![]() =
=![]() π,
π,
即B点经过的路径长为![]() .
.

练习册系列答案
相关题目