题目内容
如图所示,已知抛物线y=| 1 | 4 |
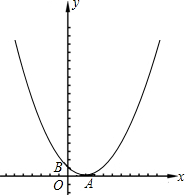 象上,且以BC为直径的⊙M恰好经过顶点A.
象上,且以BC为直径的⊙M恰好经过顶点A.(1)求k的值;
(2)求点C的坐标;
(3)若点P的纵坐标为t,且点P在该抛物线的对称轴l上运动,试探索:
①当S1<S<S2时,求t的取值范围(其中:S为△PAB的面积,S1为△OAB的面积,S2为四边形OACB的面积);
②当t取何值时,点P在⊙M上.(写出t的值即可)
分析:(1)由于抛物线的图象经过点B,那么点B的坐标满足该抛物线的解析式,将其代入即可求得k的值.
(2)若⊙M经过点A,则∠BAC必为直角(圆周角定理),过C作x轴的垂线,设垂足为D,那么△BAO∽△ACD,可设出点C的坐标,根据相似三角形所得比例线段,即可得到点C横、纵坐标的关系式,联立抛物线的解析式即可求得C点的坐标.
(3)①由于O、A、B、C四点的坐标已经确定,所以S1、S2都可求出,△ABP中,以|t|为底,B点横坐标为高,即可得到S,即S=|t|×
×2=|t|,因此S1<|t|<S2,将S1、S2的值代入上式,然后求出t的取值范围.(注意t应该分正、负两种情况考虑)
②若P在⊙M上,∠BPC=90°,即△BPC是直角三角形,可用坐标系两点间的距离公式求出△BPC的三边长,然后利用勾股定理求出t的值.
(2)若⊙M经过点A,则∠BAC必为直角(圆周角定理),过C作x轴的垂线,设垂足为D,那么△BAO∽△ACD,可设出点C的坐标,根据相似三角形所得比例线段,即可得到点C横、纵坐标的关系式,联立抛物线的解析式即可求得C点的坐标.
(3)①由于O、A、B、C四点的坐标已经确定,所以S1、S2都可求出,△ABP中,以|t|为底,B点横坐标为高,即可得到S,即S=|t|×
| 1 |
| 2 |
②若P在⊙M上,∠BPC=90°,即△BPC是直角三角形,可用坐标系两点间的距离公式求出△BPC的三边长,然后利用勾股定理求出t的值.
解答: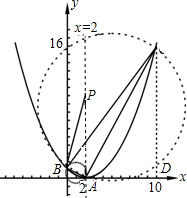 解:(1)∵点B(0,1)在y=
解:(1)∵点B(0,1)在y=
x2-x+k的图象上,
∴1=
×02-0+k,(2分)
∴k=1.(3分)
(2)由(1)知抛物线为:
y=
x2-x+1即y=
(x-2)2,
∴顶点A为(2,0),(4分)
∴OA=2,OB=1;
过C(m,n)作CD⊥x轴于D,则CD=n,OD=m,
∴AD=m-2,
由已知得∠BAC=90°,(5分)
∴∠CAD+∠BAO=90°,又∠BAO+∠OBA=90°,
∴∠OBA=∠CAD,
∴Rt△OAB∽Rt△DCA,
∴
=
,即
=
(或tan∠OBA=tan∠CAD,
=
,即
=
),(6分)
∴n=2(m-2);
又∵点C(m,n)在y=
(x-2)2上,
∴n=
(m-2)2,
∴2(m-2)=
(m-2)2,
即8(m-2)(m-10)=0,
∴m=2或m=10;当m=2时,n=0,当m=10时,n=16;(7分)
∴符合条件的点C的坐标为(2,0)或(10,16).(8分)
(3)①依题意得,点C(2,0)不符合条件,
∴点C为(10,16)
此时S1=
OA×OB=1,
S2=SBODC-S△ACD=21;(9分)
又∵点P在函数y=
(x-2)2图象的对称轴x=2上,
∴P(2,t),AP=|t|,
∴S=
OA×AP=AP=|t|(10分)
∵S1<S<S2,
∴当t≥0时,S=t,
∴1<t<21.(11分)
∴当t<0时,S=-t,
∴-21<t<-1
∴t的取值范围是:1<t<21或-21<t<-1(12分)
②t=0,1,17(14分)
 解:(1)∵点B(0,1)在y=
解:(1)∵点B(0,1)在y=| 1 |
| 4 |
∴1=
| 1 |
| 4 |
∴k=1.(3分)
(2)由(1)知抛物线为:
y=
| 1 |
| 4 |
| 1 |
| 4 |
∴顶点A为(2,0),(4分)
∴OA=2,OB=1;
过C(m,n)作CD⊥x轴于D,则CD=n,OD=m,
∴AD=m-2,
由已知得∠BAC=90°,(5分)
∴∠CAD+∠BAO=90°,又∠BAO+∠OBA=90°,
∴∠OBA=∠CAD,
∴Rt△OAB∽Rt△DCA,
∴
| AD |
| OB |
| CD |
| OA |
| m-2 |
| 1 |
| n |
| 2 |
| OA |
| OB |
| CD |
| AD |
| 2 |
| 1 |
| n |
| m-2 |
∴n=2(m-2);
又∵点C(m,n)在y=
| 1 |
| 4 |
∴n=
| 1 |
| 4 |
∴2(m-2)=
| 1 |
| 4 |
即8(m-2)(m-10)=0,
∴m=2或m=10;当m=2时,n=0,当m=10时,n=16;(7分)
∴符合条件的点C的坐标为(2,0)或(10,16).(8分)
(3)①依题意得,点C(2,0)不符合条件,
∴点C为(10,16)
此时S1=
| 1 |
| 2 |
S2=SBODC-S△ACD=21;(9分)
又∵点P在函数y=
| 1 |
| 4 |
∴P(2,t),AP=|t|,
∴S=
| 1 |
| 2 |
∵S1<S<S2,
∴当t≥0时,S=t,
∴1<t<21.(11分)
∴当t<0时,S=-t,
∴-21<t<-1
∴t的取值范围是:1<t<21或-21<t<-1(12分)
②t=0,1,17(14分)
点评:此题考查了二次函数解析式的确定、圆周角定理、图形面积的求法、不等式以及相似三角形的性质等相关知识,综合性强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C. BC交抛物线于点P.
BC交抛物线于点P.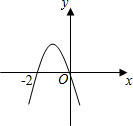 如图所示,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则2a-3b
如图所示,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则2a-3b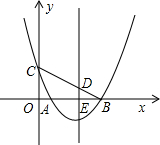 如图所示,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),抛物线的对称轴x=2交x轴于点E.
如图所示,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),抛物线的对称轴x=2交x轴于点E.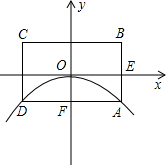 (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)