题目内容
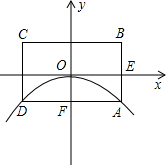 (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)(1)求此抛物线的解析式.
(2)过点P作CB所在直线的垂线,垂足为点R,
①求证:PF=PR;
②是否存在点P,使得△PFR为等边三角形?若存在,求出点P的坐标;若不存在,请说明理由;
③延长PF交抛物线于另一点Q,过Q作BC所在直线的垂线,垂足为S,试判断△RSF的形状.
分析:(1)根据题意能判断出点O是矩形ABCD的对角线交点,因此D、B关于原点对称,A、B关于x轴对称,得到A、D的坐标后,利用待定系数法可确定抛物线的解析式.
(2)①首先根据抛物线的解析式,用一个未知数表示出点P的坐标,然后表示出PF、RF的长,两者进行比较即可得证;
②首先表示RF的长,若△PFR为等边三角形,则满足PF=PR=FR,列式求解即可;
③根据①的思路,不难看出QF=QS,若连接SF、RF,那么△QSF、△PRF都是等腰三角形,先用∠SQF、∠RPF表示出∠DFS、∠RFP的和,用180°减去这个和值即可判断出△RSF的形状.
(2)①首先根据抛物线的解析式,用一个未知数表示出点P的坐标,然后表示出PF、RF的长,两者进行比较即可得证;
②首先表示RF的长,若△PFR为等边三角形,则满足PF=PR=FR,列式求解即可;
③根据①的思路,不难看出QF=QS,若连接SF、RF,那么△QSF、△PRF都是等腰三角形,先用∠SQF、∠RPF表示出∠DFS、∠RFP的和,用180°减去这个和值即可判断出△RSF的形状.
解答:解:(1)∵抛物线的顶点为坐标原点,
∴A、D关于抛物线的对称轴对称;
∵E是AB的中点,
∴O是矩形ABCD对角线的交点,又B(2,1)
∴A(2,-1)、D(-2,-1);
由于抛物线的顶点为(0,0),可设其解析式为:y=ax2,则有:
4a=-1,a=-
∴抛物线的解析式为:y=-
x2.
(2)①证明:由抛物线的解析式知:P(a,-
a2),而R(a,1)、F(0,-1),
则:PF=
=
=
a2+1,PR=1-(-
a2)=
a2+1.
∴PF=PR.
②由①得:RF=
;
若△PFR为等边三角形,则RF=PF=PR,得:
=
a2+1,即:
a4-
a2-3=0,得:
a2=-4(舍去),a2=12;
∴a=±2
,-
a2=-3;
∴存在符合条件的P点,坐标为(2
,-3)、(-2
,-3).
③同①可证得:QF=QS;
在等腰△SQF中,∠1=
(180°-∠SQF);
同理,在等腰△RPF中,∠2=
(180°-∠RPF);
∵QS⊥BC、PR⊥BC,
∴QS∥PR,∠SQP+∠RPF=180°
∴∠1+∠2=
(360°-∠SQF-∠RPF)=90°
∴∠SFR=180°-∠1-∠2=90°,
即△SFR是直角三角形.
∴A、D关于抛物线的对称轴对称;
∵E是AB的中点,
∴O是矩形ABCD对角线的交点,又B(2,1)
∴A(2,-1)、D(-2,-1);
由于抛物线的顶点为(0,0),可设其解析式为:y=ax2,则有:
4a=-1,a=-
| 1 |
| 4 |
∴抛物线的解析式为:y=-
| 1 |
| 4 |
(2)①证明:由抛物线的解析式知:P(a,-
| 1 |
| 4 |
则:PF=
(a-0)2+(-
|
|
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴PF=PR.
②由①得:RF=
| a2+4 |
若△PFR为等边三角形,则RF=PF=PR,得:
| a2+4 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 2 |

a2=-4(舍去),a2=12;
∴a=±2
| 3 |
| 1 |
| 4 |
∴存在符合条件的P点,坐标为(2
| 3 |
| 3 |
③同①可证得:QF=QS;
在等腰△SQF中,∠1=
| 1 |
| 2 |
同理,在等腰△RPF中,∠2=
| 1 |
| 2 |
∵QS⊥BC、PR⊥BC,
∴QS∥PR,∠SQP+∠RPF=180°
∴∠1+∠2=
| 1 |
| 2 |
∴∠SFR=180°-∠1-∠2=90°,
即△SFR是直角三角形.
点评:该题考查了二次函数的性质及解析式的确定、矩形的性质、特殊三角形的判定等知识,综合性较强.在解答题目时,要注意数形结合,并灵活应用前面小题中证得的结论.

练习册系列答案
相关题目
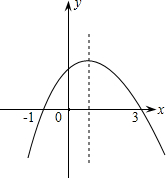 (2012•衡阳)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
(2012•衡阳)如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法: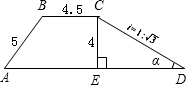 (2012•衡阳)如图,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD.(i=CE:ED,单位:m)
(2012•衡阳)如图,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD.(i=CE:ED,单位:m)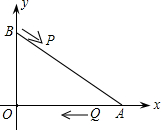 (2012•衡阳)如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<
(2012•衡阳)如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<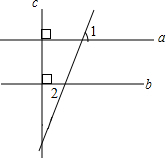 (2012•衡阳)如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )
(2012•衡阳)如图,直线a⊥直线c,直线b⊥直线c,若∠1=70°,则∠2=( )