题目内容
 如图所示,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),抛物线的对称轴x=2交x轴于点E.
如图所示,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),抛物线的对称轴x=2交x轴于点E.(1)求交点A的坐标及抛物线的函数关系式;
(2)在平面直角坐标系xOy中是否存在点P,使点P与A,B,C三点构成一个平行四边形?若存在,请直接写出点P坐标;若不存在,请说明理由;
(3)连接CB交抛物线对称轴于点D,在抛物线上是否存在一点Q,使得直线CQ把四边形DEOC分成面积比为1:7的两部分?若存在,请求出点Q坐标;若不存在,请说明理由.
分析:(1)把点B的坐标为(3,0)代入抛物线y=x2+bx+c得到b,c的关系式;又因为抛物线的对称轴x=2,可求出b的值,进而求出求交点A的坐标及抛物线的函数关系式;
(2)分别以AC,AB为对角线各可求得一点,再以AC,AB为边求得一点;
(3)此小题要分类讨论:当分的图象左边部分是三角形,右边部分是四边形或当分的图象左边部分是四边形,右边部分是三角形时分别计算满足题意的Q值即可.
(2)分别以AC,AB为对角线各可求得一点,再以AC,AB为边求得一点;
(3)此小题要分类讨论:当分的图象左边部分是三角形,右边部分是四边形或当分的图象左边部分是四边形,右边部分是三角形时分别计算满足题意的Q值即可.
解答:解:(1)∵抛物线y=x2+bx+c与x轴交点B(3,0),对称轴x=2,
∴
,
解得:
∴抛物线的函数关系式为y=x2-4x+3,
令y=0,则x2-4x+3=0,
解得:x1=1,x2=3.
∴抛物线与x轴另一个交点A的坐标(1,0);
(2)存在,
满足条件的点P有3个,分别为(-2,3),(2,3),(4,-3).
(3)存在,
①直线CQ与OE相交,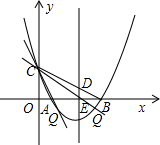
当x=0时,y=x2-4x+3=3,
∴点C的坐标为(0,3),
过点C、Q的直线关系式y=-9x+3
∴
解得:
,
∴Q(-5,48);
②直线CQ与DE相交,
过点C、Q的直线关系式y=-
x+3,
∴
,
∴
,
∴Q(
,-
).
综上所述符合条件的Q有两个坐标分别是(-5,48);(
,-
).
∴
|
解得:
|
∴抛物线的函数关系式为y=x2-4x+3,
令y=0,则x2-4x+3=0,
解得:x1=1,x2=3.
∴抛物线与x轴另一个交点A的坐标(1,0);
(2)存在,
满足条件的点P有3个,分别为(-2,3),(2,3),(4,-3).
(3)存在,
①直线CQ与OE相交,

当x=0时,y=x2-4x+3=3,
∴点C的坐标为(0,3),
过点C、Q的直线关系式y=-9x+3
∴
|
解得:
|
∴Q(-5,48);
②直线CQ与DE相交,
过点C、Q的直线关系式y=-
| 5 |
| 4 |
∴
|
∴
|
∴Q(
| 11 |
| 4 |
| 7 |
| 16 |
综上所述符合条件的Q有两个坐标分别是(-5,48);(
| 11 |
| 4 |
| 7 |
| 16 |
点评:此题考查了二次函数与一次函数,四边形的综合知识,解题的关键是要注意数形结合思想的应用.此题属于中考中的压轴题,难度较大,知识点考查的较多而且联系密切,需要学生认真审题.

练习册系列答案
相关题目
 如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C. BC交抛物线于点P.
BC交抛物线于点P. 如图所示,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则2a-3b
如图所示,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则2a-3b (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)