题目内容
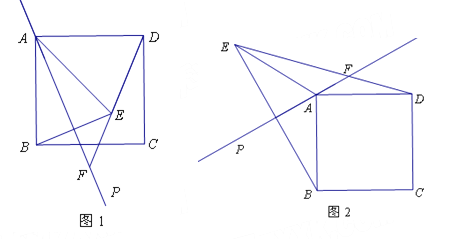
【题目】如图,在四边形ABCD中,ADBC,E是AB 的中点,连接DE并延长交CB 的延长线于点F,点G在BC边上,且GDF ADF .
(1)求证:ADE ≌ BFE ;
(2)连接EG ,判断EG 与DF 的位置关系,并说明理由;
(3)若CDF 90,DF 4,CD 3 , CF 5 ,求RtCDF的三条角平分线的交点O 到边CF的距离.

【答案】(1)详见解析;(2)详见解析;(3)1.
【解析】
(1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE;
(2)∠GDF=∠ADE,以及(1)得出的∠ADE=∠BFE,等量代换得到∠GDF=∠BFE,利用等角对等边得到GF=GD,即三角形GDF为等腰三角形,再由(1)得到DE=FE,即GE为底边上的中线,利用三线合一即可得到GE与DF垂直.
(3)根据直角三角形的内切圆的半径解答即可.
(1)证明:∵AD∥BC,∴∠ADE=∠BFE,
∵E为AB的中点,∴AE=BE,
在△ADE和△BFE中,
 ,
,
∴△ADE≌△BFE(AAS);

(2)EG与DF的位置关系是EG垂直平分DF,
理由为:连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△ADE≌△BFE得:DE=FE,即GE为DF上的中线,
∴GE垂直平分DF.
(3)∵Rt△CDF的三条角平分线的交点O到边CF的距离即是△CDF的内切圆的半径,
∵∠CDF=90°,DF=4,CD=3,CF=5,
设△CDF的内切圆半径为r,
∵在Rt△CDF中,∠CDF=90°,DF=4,CD=3,CF=5,
∴S△CDF=![]() DCDF=
DCDF=![]() r(DF+DC+CF),
r(DF+DC+CF),
∴r=![]() =
=![]()
=1.
即Rt△CDF的三条角平分线的交点O到边CF的距离是1.

 阅读快车系列答案
阅读快车系列答案