题目内容
有四条线段,长度分别是2cm,3cm,4cm,5cm,从中任取三条,能构成三角形的概率是
- A.25%
- B.50%
- C.75%
- D.100%
C
分析:由四条线段中任意取3条,是一个列举法求概率问题,是无放回的问题,共有4×3×2=24种可能结果,每种结果出现的机会相同,其中不满足两边之和>第三边的有:2cm,3cm,5cm;2cm,5cm,3cm;3cm,2cm,5cm;3cm,5cm,2cm;5cm,2cm,3cm;5cm,3cm,2cm共6种,则满足的有24-6=18种,因而就可求出概率.
解答:P(任取三条,能构成三角形)=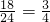 =75%.
=75%.
故选C.
点评:本题是一个列举法求概率与三角形的三边关系相结合的题目;情况较少可用列举法求概率,采用列举法解题的关键是找到所有存在的情况.用到的知识点为:概率=所求情况数与总情况数之比.组成三角形的两小边之和大于最大的边长.
分析:由四条线段中任意取3条,是一个列举法求概率问题,是无放回的问题,共有4×3×2=24种可能结果,每种结果出现的机会相同,其中不满足两边之和>第三边的有:2cm,3cm,5cm;2cm,5cm,3cm;3cm,2cm,5cm;3cm,5cm,2cm;5cm,2cm,3cm;5cm,3cm,2cm共6种,则满足的有24-6=18种,因而就可求出概率.
解答:P(任取三条,能构成三角形)=
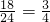 =75%.
=75%.故选C.
点评:本题是一个列举法求概率与三角形的三边关系相结合的题目;情况较少可用列举法求概率,采用列举法解题的关键是找到所有存在的情况.用到的知识点为:概率=所求情况数与总情况数之比.组成三角形的两小边之和大于最大的边长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目