Question

【题目】已知点A（-2，1），B（0，4），C（8，16），O（0，0），P（m，n），抛物线y=ax2（a≠0）经过A，B，C，其中的一点，

（1）求抛物线y=ax2（a≠0）的解析式；

（2）若直线y=mx（m≠0）与直线y=nx（n≠0）分别经过点A与点C，判断点P（m，n）是否在反比例函数y=-的图象上；

（3）若点P（m，n）是反比例函数y=-的图象上任一点，且直线y=mx（m≠0）与直线y=nx（n≠0）分别与抛物线y=ax2（a≠0）交于点M，点N（不同于原点），求证：M，B，N三点在一条直线上．

Answer 1

【答案】（1）y=x2；（2）点P在反比例函数y=-的图象上；（3）证明见解析

【解析】

（1）根据抛物线y=ax2的顶点坐标为（0,0），可判断图象不过点B，分别将点A的坐标或点C的坐标代入解析式中即可求出抛物线的解析式；

（2）将点A的坐标代入y=mx中即可求出m的值，将点C的坐标代入y=nx即可求出n的值，从而判断结论；

（3）分别联立方程求出点M和点N的坐标，利用待定系数法求出直线MN的解析式，然后判断点B的坐标是否满足该解析式即可得出结论．

解：（1）∵抛物线y=ax2的顶点坐标为（0,0）

∴抛物线一定不过点B

把A（-2，1）代入y=ax2，得a=，

把C（8，16）代入y=ax2，得a=，

故该抛物线解析式为：y=x2．

（2）∵直线y=mx（m≠0）与直线y=nx（n≠0）分别经过点A（-2，1）与点C（8，16），

∴1=-2m，16=8n．

∴m=-，n=2．

∴点P的坐标是（-，2）．

把x=-代入y=-，得y=2．

∴点P在反比例函数y=-的图象上．

（3）证明：∵点M，点N分别是直线y=mx（m≠0）与直线y=nx（n≠0）分别与抛物线y=ax2（a≠0）的交点，

∴可列方程组：，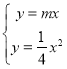

解得．

∴点M的坐标是（4m，4m2）．

同理，，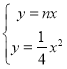

解得．

∴点N的坐标是（4n，4n2）．

设经过点M、N的直线为：y=kx+b（k≠0）．

把M（4m，4m2），N（4n，4n2）分别代入，得．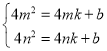

解得．

∵点P（m，n）在反比例函数y=-的图象上，

∴mn=-1．即b=-mn=-4×（-1）=4．

∴y=（m+n）x+4．

把x=0代入，得y=4，即点B（0，4）在直线MN上．

∴点M，B，N三点在一条直线上．