题目内容
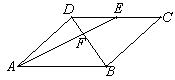
如图,平行四边形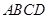 中,
中,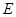 为
为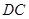 的中点,
的中点,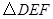 的面积为2,则△
的面积为2,则△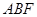 的面积为( )
的面积为( )
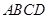 中,
中,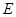 为
为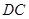 的中点,
的中点,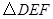 的面积为2,则△
的面积为2,则△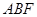 的面积为( )
的面积为( )
| A.2 | B.4 |
| C.6 | D.8 |
D
由平行四边形ABCD中,E为DC的中点,可得△DEF∽△BAF,相似比为1:2,又由相似三角形的面积比等于其相似比的平方,即可求得答案.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△DEF∽△BAF,
∴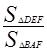 = (
= (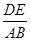 )2,
)2,
∵E为DC的中点,
∴DE=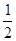 CD,
CD,
∴DE:AB=1:2,
∴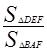 =(
=(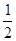 )2,
)2,
∵△DEF的面积为2,
∴△ABF的面积为8.
故选D.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△DEF∽△BAF,
∴
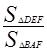 = (
= (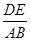 )2,
)2,∵E为DC的中点,
∴DE=
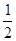 CD,
CD,∴DE:AB=1:2,
∴
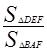 =(
=(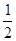 )2,
)2,∵△DEF的面积为2,
∴△ABF的面积为8.
故选D.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
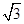 ,堤高BC=5m,则坡面AB的长度是( )
,堤高BC=5m,则坡面AB的长度是( )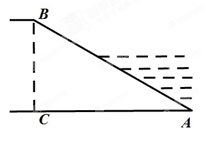
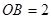 ,
,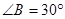 ,点C是弦AB上一动点(不与点A、B重合),连结CO并延长交⊙O于点D,连结AD.
,点C是弦AB上一动点(不与点A、B重合),连结CO并延长交⊙O于点D,连结AD.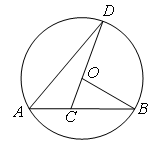
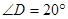 时,求
时,求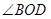 的度数;
的度数;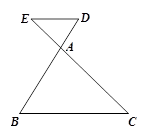
 中,DE//BC,且AE=3cm,EC=5cm,DE=6cm,则BC等于( )
中,DE//BC,且AE=3cm,EC=5cm,DE=6cm,则BC等于( )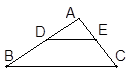

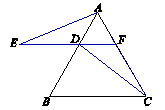
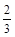 ,CH=2,求BC的长.
,CH=2,求BC的长.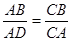 中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】
中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】 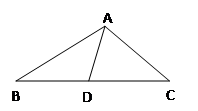
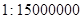 的卫星地图上,测得上海和南京的距离大约是
的卫星地图上,测得上海和南京的距离大约是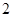 厘米.那么上海和南京的实际距离大约是 ▲ 千米.
厘米.那么上海和南京的实际距离大约是 ▲ 千米.