Question

【题目】如图，正方形ABCD的边长为1，其中弧DE、弧EF、弧FG的圆心依次为点A、B、C．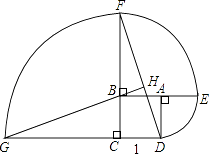
（1）求点D沿三条弧运动到点G所经过的路线长；
（2）判断直线GB与DF的位置关系，并说明理由．

Answer 1

【答案】
（1）解：根据弧长公式得所求路线长为：

=3π．

（2）解：GB⊥DF．

理由如下：

在△FCD和△GCB中，

∵ ，

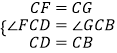∴△FCD≌△GCB（SAS），

∴∠G=∠F，

∵∠F+∠FDC=90°，

∴∠G+∠FDC=90°，

∴∠GHD=90°，

∴GB⊥DF．

【解析】（1）根据弧长的计算公式，代入运算即可．（2）先证明△FCD≌△GCB，得出∠G=∠F，从而利用等量代换可得出∠GHD=90°，即GB⊥DF．
【考点精析】本题主要考查了正方形的性质和弧长计算公式的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的才能正确解答此题．