题目内容
【题目】如图所示，抛物线y=ax2+bx+c（a≠0）的顶点坐标为点A（﹣2，3），且抛物线y=ax2+bx+c与y轴交于点B（0，2）．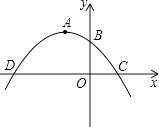
（1）求该抛物线的解析式；
（2）是否在x轴上存在点P使△PAB为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）若点P是x轴上任意一点，则当PA﹣PB最大时，求点P的坐标．
【答案】
（1）
解：∵抛物线的顶点坐标为A（﹣2，3），∴可设抛物线的解析式为y=a（x+2）2+3．
由题意得：a（0+2）2+3=2，解得：a=﹣ 
．
∴物线的解析式为y=﹣ （x+2）2+3，即y=﹣ x2﹣x+2．
（2）
解：设存在符合条件的点P，其坐标为（p，0），则
PA2=（﹣2﹣p）2+32，PB2=p2+22，AB2=（3﹣2）2+22=5
当PA=PB时，（﹣2﹣p）2+32=p2+22，解得：p=﹣ 
；
当PA=AB时，（﹣2﹣p）2+32=5，方程无实数解；
当PB=AB时，p2+22=5，解得p=±1．
∴x轴上存在符合条件的点P，其坐标为（﹣ ，0）或（﹣1，0）或（1，0）．
（3）
解：∵PA﹣PB≤AB，
∴当A、B、P三点共线时，可得PA﹣PB的最大值，这个最大值等于AB，此时点P是直线AB与x轴的交点．
设直线AB的解析式为y=kx+b，则：
，解得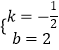 
．
∴直线AB的解析式为y=﹣ 
x+2，
当y=﹣ x+2=0时，解得x=4．
∴当PA﹣PB最大时，点P的坐标是（4，0）．
【解析】（1）通过读题可以看出抛物线y=ax2+bx+c（a≠0）的顶点坐标为点A（﹣2，3），且经过B点，所以直接将抛物线的解析式设为顶点式，然后代入B点的坐标求解即可．（2）首先设出P点的坐标，根据坐标系两点间的距离公式分别求出PA、PB、AB的长度（或表达式），然后分PA=PB、PA=AB、PB=AB三种情况列方程求解即可．（3）当P、A、B三点不共线时，PA﹣PB＜AB（三角形三边关系定理），三点共线时，PA﹣PB=AB，综合来看：PA﹣PB≤AB，所以当PA﹣PB的值最大时，P、A、B三点共线，因此只需求出直线AB的解析式，该直线与x轴的交点即为符合条件的P点．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．
