题目内容
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P. 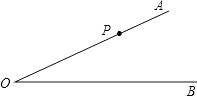
(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
【答案】
(1)解:过点P作PC⊥OB,垂足为C,
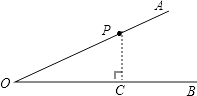
则∠OCP=90°.
∵∠AOB=30°,OP=24cm,
∴PC= ![]() OP=12cm.
OP=12cm.
当r=12cm时,r=PC,
∴⊙P与OB相切,
即⊙P与OB位置关系是相切.
(2)当⊙P与OB相离时,r<PC,
∴r需满足的条件是:0cm<r<12cm.
【解析】(1)过点P作PC⊥OB,垂足为C根据含30度角的直角三角形性质求出PC,得出PC=r,则得出⊙P与OB位置关系是相切;(2)根据相切时半径=12,再根据当r<d时相离,即可求出答案.
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.

练习册系列答案
相关题目
【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?