题目内容
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且![]() =
=![]() .
.
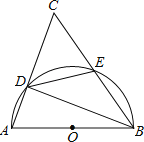
(1)试判断△ABC的形状,并说明理由.
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
【答案】(1)△ABC为等腰三角形;(2)![]() .
.
【解析】
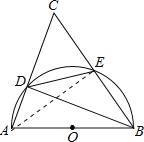
试题分析:(1)连结AE,如图,根据圆周角定理,由![]() =
=![]() 得∠DAE=∠BAE,由AB为直径得∠AEB=90°,根据等腰三角形的判定方法即可得△ABC为等腰三角形;
得∠DAE=∠BAE,由AB为直径得∠AEB=90°,根据等腰三角形的判定方法即可得△ABC为等腰三角形;
(2)由等腰三角形的性质得BE=CE=![]() BC=6,再在Rt△ABE中利用勾股定理计算出AE=8,接着由AB为直径得到∠ADB=90°,则可利用面积法计算出BD=
BC=6,再在Rt△ABE中利用勾股定理计算出AE=8,接着由AB为直径得到∠ADB=90°,则可利用面积法计算出BD=![]() ,然后在Rt△ABD中利用勾股定理计算出AD=
,然后在Rt△ABD中利用勾股定理计算出AD=![]() ,再根据正弦的定义求解.
,再根据正弦的定义求解.
解:(1)△ABC为等腰三角形.理由如下:
连结AE,如图,
∵![]() =
=![]() ,
,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴BE=CE=![]() BC=
BC=![]() ×12=6,
×12=6,
在Rt△ABE中,∵AB=10,BE=6,
∴AE=![]() =8,
=8,
∵AB为直径,
∴∠ADB=90°,
∴![]() AEBC=
AEBC=![]() BDAC,
BDAC,
∴BD=![]() =
=![]() ,
,
在Rt△ABD中,∵AB=10,BD=![]() ,
,
∴AD=![]() =
=![]() ,
,
∴sin∠ABD=![]() =
=![]() =
=![]() .
.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目