题目内容
 已知:如图,在矩形ABCD中,BC=2,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( )
已知:如图,在矩形ABCD中,BC=2,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( )A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据已知条件,先求Rt△AED的面积,再证明△ECD的面积与它相等.
解答: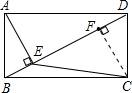 解:如图:
解:如图:
过点C作CF⊥BD于F.
∵矩形ABCD中,BC=2,AE⊥BD,
∴∠ABE=∠CDF=60°,AB=CD,AD=BC=2,∠AEB=∠CFD=90°.
∴△ABE≌△CDF.
∴AE=CF.
∴S△AED=
ED•AE,S△ECD=
ED•CF
∴S△AED=S△CDE∵AE=1,DE=
,
∴△ECD的面积是
.故选C.
 解:如图:
解:如图:过点C作CF⊥BD于F.
∵矩形ABCD中,BC=2,AE⊥BD,
∴∠ABE=∠CDF=60°,AB=CD,AD=BC=2,∠AEB=∠CFD=90°.
∴△ABE≌△CDF.
∴AE=CF.
∴S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AED=S△CDE∵AE=1,DE=
| 3 |
∴△ECD的面积是
| ||
| 2 |
点评:此题考查了学生的识图能力,解题的关键是要注意问题的转化.此题还考查了直角三角形的性质,直角三角形中,30°角所对的直角边是斜边的一半.

练习册系列答案
相关题目
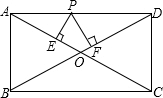 已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )
已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )A、PE+PF=
| ||||
B、
| ||||
| C、PE+PF=5 | ||||
| D、3<PE+PF<4 |
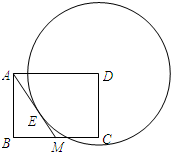 已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E,
已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E,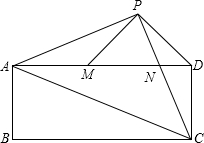 已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M. 已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E,
已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E,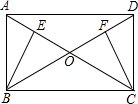 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.