Question

已知，如图，在矩形ABCD中，P是边AD上的动点，PE垂直AC于E，PF垂直BD于F，如果AB=3，AD=4，那么（　　）

• A、PE+PF=

  12

  5

• B、

  12

  5

  ＜PE+PF＜

  13

  5

• C、PE+PF=5
• D、3＜PE+PF＜4

Answer 1

分析：用两种方法表示出△AOD的面积，即可得到所求线段与其他易求得的线段的关系．

解答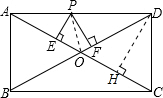：解：作DH⊥AC，连接OP．
则△OAD的面积就是OA×DH×0.5．
把这个三角形分成两个小三角形面积就是OA×PE×0.5+OD×PF×0.5．
两式相等，列出等式可得：DH=PE+PF．
∵Rt△ACD中，AD=4，CD=3，
∴AC=5，
∴DH=

AD•CD

AC

=

12

5

．
故选A．

点评：本题的关键是利用直角三角形面积的两种算法，即一种是两直角边的积的一半；一种是底边乘高的一半．