题目内容
 已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E,
已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E,求⊙D的半径.
分析:连接DE.根据切线的性质得DE⊥AM,根据矩形的性质可证明△ADE∽△MAB,则
=
,由已知可求出AM的长,进而得出⊙D的半径.
| DE |
| AD |
| AB |
| AM |
解答:解:连接DE.(1分)
∵⊙D与直线AM相切于点E,∴DE⊥AM.(1分)
在矩形ABCD中,
∵AD∥BC,∴∠DAE=∠AMB.(1分)
∵∠AED=∠B=90°,∴△ADE∽△MAB.(1分)
∴
=
.(1分)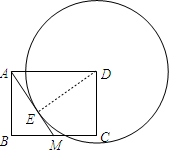
∵AB=3,BC=AD=4,BM=CM=2,∴AM=
.(1分)
∴
=
.解得DE=
,即⊙D的半径为
.(1分)
∵⊙D与直线AM相切于点E,∴DE⊥AM.(1分)
在矩形ABCD中,
∵AD∥BC,∴∠DAE=∠AMB.(1分)
∵∠AED=∠B=90°,∴△ADE∽△MAB.(1分)
∴
| DE |
| AD |
| AB |
| AM |

∵AB=3,BC=AD=4,BM=CM=2,∴AM=
| 13 |
∴
| DE |
| 4 |
| 3 | ||
|
| 12 |
| 13 |
| 13 |
| 12 |
| 13 |
| 13 |
点评:本题考查了切线的性质、矩形的性质以及相似三角形的判定和性质,是基础知识要熟练掌握.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )
已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )A、PE+PF=
| ||||
B、
| ||||
| C、PE+PF=5 | ||||
| D、3<PE+PF<4 |
 已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M. 已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E,
已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E, 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.