题目内容
 已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.(1)若AP=
| 5 |
| 1 |
| 3 |
(2)若CD=PM,求证:AC=AP+PN.
分析:(1)根据勾股定理求出AC,设AB=x,BC=3x,在Rt△ABC中根据勾股定理求出,求出AB、BC、即可求出答案;
(2)延长AP,CD交于Q,求出∠1=∠2,∠3=∠4,根据ASA证△APM≌△CPD,得出DP=PM=CD,求出∠Q=∠6,推出AC=AQ=AP+PQ,根据AS证△APN≌△CPQ,推出PQ=PN,即可得出答案.
(2)延长AP,CD交于Q,求出∠1=∠2,∠3=∠4,根据ASA证△APM≌△CPD,得出DP=PM=CD,求出∠Q=∠6,推出AC=AQ=AP+PQ,根据AS证△APN≌△CPQ,推出PQ=PN,即可得出答案.
解答:(1)解:∵AP⊥CP且AP=CP,
∴△APC为等腰直角三角形,
∵AP=
,
∴AC=
,
∵AB=
BC,
∴设AB=x,BC=3x,
∴在Rt△ABC中,
x2+(3x)2=10,
10x2=10,
x=1,
∴SABCD=AB•BC=1×3=3;
(2)解:延长AP,CD交于Q,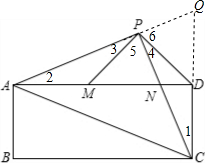
∵∠1+∠CND=∠2+∠PNA=90°,
且∠CND=∠ANP,
∴∠1=∠2,
又∠3+∠5=∠4+∠5=90°,
∴∠3=∠4,
在△APM和△CPD中
∵
,
∴△APM≌△CPD(ASA),
∴DP=PM,
又∵CD=PM,
∴CD=PD,
∴∠1=∠4=∠3,
∵∠1+∠Q=∠3+∠6=90°
∴∠Q=∠6
∴DQ=DP=CD
∴D为CQ中点,
又∵AD⊥CQ
∴AC=AQ=AP+PQ,
在△APN和△CPQ中
∵
,
∴△APN≌△CPQ(ASA),
∴PQ=PN
∴AC=AP+PQ=AP+PN.
∴△APC为等腰直角三角形,
∵AP=
| 5 |
∴AC=
| 10 |
∵AB=
| 1 |
| 3 |
∴设AB=x,BC=3x,
∴在Rt△ABC中,
x2+(3x)2=10,
10x2=10,
x=1,
∴SABCD=AB•BC=1×3=3;
(2)解:延长AP,CD交于Q,

∵∠1+∠CND=∠2+∠PNA=90°,
且∠CND=∠ANP,
∴∠1=∠2,
又∠3+∠5=∠4+∠5=90°,
∴∠3=∠4,
在△APM和△CPD中
∵
|
∴△APM≌△CPD(ASA),
∴DP=PM,
又∵CD=PM,
∴CD=PD,
∴∠1=∠4=∠3,
∵∠1+∠Q=∠3+∠6=90°
∴∠Q=∠6
∴DQ=DP=CD
∴D为CQ中点,
又∵AD⊥CQ
∴AC=AQ=AP+PQ,
在△APN和△CPQ中
∵
|
∴△APN≌△CPQ(ASA),
∴PQ=PN
∴AC=AP+PQ=AP+PN.
点评:本题考查了矩形的性质,全等三角形的性质和判定,三角形的内角和定理,等腰三角形的性质和判定,线段垂直平分线定理等知识点,主要考查学生综合运用性质和定理进行推理的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )
已知,如图,在矩形ABCD中,P是边AD上的动点,PE垂直AC于E,PF垂直BD于F,如果AB=3,AD=4,那么( )A、PE+PF=
| ||||
B、
| ||||
| C、PE+PF=5 | ||||
| D、3<PE+PF<4 |
 已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E,
已知,如图,在矩形ABCD中,M是边BC的中点,AB=3,BC=4,⊙D与直线AM相切于点E, 已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E,
已知:如图,在矩形ABCD中,AB=4,AD=10,F是AD上一点,CF⊥EF于点F交AB于点E, 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F,请你判断BE与CF的大小关系,并说明你的理由.