题目内容
【题目】已知∠AOB=90°,∠COD=30°.
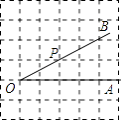
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是;
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数 . 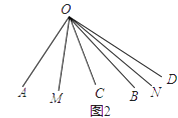
【答案】
(1)60°
(2)60、90、150,60°
【解析】解:(1)∠BOD=∠AOB﹣∠AOD=∠AOB﹣∠COD=90°﹣30°=60°.
故答案为:60°.(2)①∵0<n<180,
∴分三种情况.
a:点D在射线0B上,∠AOC=∠AOB﹣∠COD=90°﹣30°=60°;
b:点C在射线OB上,∠AOC=∠AOB=90°;
c:点D在AO的延长线上,∠AOC=180°﹣∠COD=180°﹣30°=150°.
综上得n为60、90、150.
故答案为:60、90、150.②∵∠AOC=n°,OM平分∠AOC,
∴∠AOM= ![]() n°,
n°,
∠AOD=∠AOC+∠COD=n°+30°,
∠BOD=∠AOD﹣∠AOB=n°+30°﹣90°=n°﹣60°,
∵ON平分∠BOD,
∴∠DON= ![]() ∠BOD=
∠BOD= ![]() ×(n°﹣60°)=
×(n°﹣60°)= ![]() n°﹣30°,
n°﹣30°,
∠MON=∠AOD﹣∠AOM﹣∠DON=n°+30°﹣ ![]() n°﹣(
n°﹣( ![]() n°﹣30°)=60°
n°﹣30°)=60°
(1)根据,∠BOD=∠AOB﹣∠AOD=∠AOB﹣∠COD,而∠AOD=∠COD=30°,代入即可求出结论;
(2)①0<n<180,在旋转的过程中,能够发现∠COD的一边与∠AOB的一边垂直共有三种情况,分别求出每种情况下旋转的度数即可;
②∠AOC=n°,OM平分∠AOC,根据角平分线的定义及角与角之间的关系,将直接求∠MON得度数转换成求∠AOM,∠DON的度数,再依照角的关系即可求得结论.