题目内容
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC和CD于点P,Q.
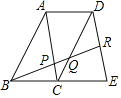
(1)求证:△ABP∽△DQR;
(2)求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据平行线的性质可证明两三角形相似;
(2)根据平行四边形的性质及三角形中位线定理得:BP=PR,则CP=![]() RE,证明△CPQ∽△DRQ,可得
RE,证明△CPQ∽△DRQ,可得![]() ,由(1)中的相似列比例式可得结论.
,由(1)中的相似列比例式可得结论.
(1)∵四边形ABCD和四边形ACED都是平行四边形,
∴AB∥CD,AC∥DE,
∴∠BAC=∠ACD,∠ACD=∠CDE,
∴∠BAC=∠QDR,
∵AB∥CD,
∴∠ABP=∠DQR,
∴△ABP∽△DQR;
(2)∵四边形ABCD和四边形ACED都是平行四边形,
∴AD=BC,AD=CE,
∴BC=CE,
∵CP∥RE,
∴BP=PR,
∴CP=![]() RE,∵点R为DE的中点,
RE,∵点R为DE的中点,
∴DR=RE,
∴![]() ,
,
∵CP∥DR,
∴△CPQ∽△DRQ,
∴![]() ,
,
∴![]() ,
,
由(1)得:△ABP∽△DQR,
∴![]() .
.

练习册系列答案
相关题目