题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.

【答案】(1)详见解析;(2)BC与⊙P相切,理由见解析.
【解析】
试题分析:(1)根据题目要求作出图形即可,如图所示;(2)BC与⊙P相切,理由为:过P作PD⊥BC,交BC于点P,利用角平分线定理得到PD=PA,而PA为圆P的半径,即可得BC与⊙P相切.
试题解析:(1)如图所示,⊙P为所求的圆;
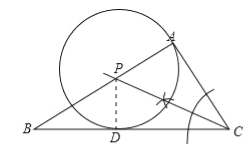
(2)BC与⊙P相切,理由为:
过P作PD⊥BC,交BC于点P,
∵CP为∠ACB的平分线,且PA⊥AC,PD⊥CB,
∴PD=PA,
∵PA为⊙P的半径.
∴BC与⊙P相切.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目