Question

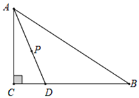
【题目】如图，Rt△ABC中，∠C＝90°，AC＝24，点D在边BC上， CD＝10，BD＝26．点P是线段AD上一动点，当半径为12的⊙P与△ABC的一边相切时，AP的长为_____．

Answer 1

【答案】或

【解析】

根据勾股定理得到AB＝＝12，AD＝＝26，当⊙P于BC相切时，点P到BC的距离＝12，过P作PH⊥BC于H，则PH＝12，当⊙P于AB相切时，点P到AB的距离＝12，根据相似三角形的性质即可得到结论．

∵在Rt△ABC中，∠C＝90°，AC＝24，BD＋CD＝36，

∴AB＝＝12，

在Rt△ADC中，∠C＝90°，AC＝24，CD＝10，

∴AD＝＝26，

当⊙P于BC相切时，点P到BC的距离＝12，

过P作PH⊥BC于H

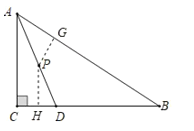
则PH＝12，

∵∠C＝90°，

∴AC⊥BC，

∴PH∥AC，

∴△DPH∽△DAC，

∴，

∴，

∴PD＝13，

∴AP＝13；

当⊙P于AB相切时，点P到AB的距离＝12，

过P作PG⊥AB于G，

则PG＝12，

∵AD＝BD＝26，

∴∠PAG＝∠B，

∵∠AGP＝∠C＝90°，

∴△AGP∽△BCA，

∴，

∴，

∴AP＝，

∵CD＝10＜12，

∴半径为6的⊙P不与△ABC的AC边相切，

综上所述，AP的长为或，

故答案为：或．