题目内容
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=![]() (k>0,x>0)的图像上点P(m,n)是函数图像上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
(k>0,x>0)的图像上点P(m,n)是函数图像上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
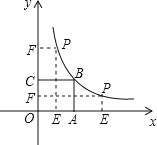
(1)求k的值;
(2)当S=![]() 时 求p点的坐标;
时 求p点的坐标;
(3)写出S关于m的关系式.
【答案】(1)k=9;(2)P(6,![]() ),(
),(![]() ,6);(3)当0<m<3时S=9-3m;当m≥3时 ,S=9-3n=9-
,6);(3)当0<m<3时S=9-3m;当m≥3时 ,S=9-3n=9-![]() .
.
【解析】分析:(1)根据反比例函数中正方形的面积与反比例系数的关系,即可求得反比例函数解析式,进而求得k的值;(2)根据S=n(m-AO)即可得到方程求解;(3)根据S=n(m-AO)即可写出函数解析式.
本题解析:(1)∵正方形OABC的面积为9,∴OA=OC=3,∴B(3,3),
又∵点B(3,3)在函数y=![]() 的图象上,∴k=9;
的图象上,∴k=9;
(2)分两种情况:①当点P在点B的左侧时,∵P(m,n)在函数y=![]() 上,
上,
∴mn=9,∴S=m(n-3)=mn-3m=![]() ,解得m=
,解得m=![]() ,∴n=6,∴点P的坐标是P(
,∴n=6,∴点P的坐标是P(![]() ,6);
,6);
②当点P在点B的右侧时,∵P(m,n)在函数y=![]() 上,∴mn=9,∴S=n(m-3)=mn-3n=
上,∴mn=9,∴S=n(m-3)=mn-3n=![]() ,解得n=
,解得n=![]() ,∴m=6,∴点P的坐标是P(6,
,∴m=6,∴点P的坐标是P(6,![]() ),综上所述:P(6,
),综上所述:P(6,![]() ),(
),(![]() ,6).
,6).
(3)当0<m<3时,点P在点B的左边,此时S=9-3m,
当m≥3时,点P在点B的右边,此时S=9-3n=9-![]() .
.

练习册系列答案
相关题目
【题目】对一批衬衣进行抽检,得到合格衬衣的频数表如下,若出售1200件衬衣,则其中次品的件数大约是( )
抽取件数(件) | 50 | 100 | 150 | 200 | 500 | 800 | 1000 |
合格频数 | 48 | 98 | 144 | 193 | 489 | 784 | 981 |
A.12B.24C.1188D.1176