题目内容
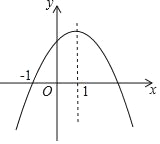
【题目】二次函数y=ax2+bx+c（a，b，c为常数，a≠0）的图象如图所示，下列结论：①abc＜0；②2a+b＜0；③b2﹣4ac=0；④8a+c＜0；⑤a：b：c=﹣1：2：3，其中正确的结论有______．
【答案】①④⑤
【解析】①∵开口向下，∴a＜0，
∵与y轴交于正半轴，∴c＞0，
∵对称轴在y轴右侧，∴b＞0，∴abc＜0，故①正确；
∵二次函数的对称轴是直线x=1，即二次函数的顶点的横坐标为x=﹣
=1，
∴2a+b=0，故②错误；
∵抛物线与x轴有两个交点，
∴b2﹣4ac＞0，故③错误；
∵b=﹣2a，∴可将抛物线的解析式化为：y=ax2﹣2ax+c（a≠0）；
由函数的图象知：当x=﹣2时，y＜0；即4a﹣（﹣4a）+c=8a+c＜0，故④正确；
∵二次函数的图象和x轴的一个交点时（﹣1，0），对称轴是直线x=1，
∴另一个交点的坐标是（3，0），
∴设y=ax2+bx+c=a（x﹣3）（x+1）=ax2﹣2ax﹣3a，
即a=a，b=﹣2a，c=﹣3a，
∴a：b：c=a：（﹣2a）：（﹣3a）=﹣1：2：3，故⑤正确；
故答案为：①④⑤．
练习册系列答案
相关题目
【题目】用
纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元.在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元.
设在同一家复印店一次复印文件的页数为
（
为非负整数）.
（1）根据题意，填写下表：
一次复印页数（页） | 5 | 10 | 20 | 30 | … |
甲复印店收费（元） |
| 2 | … | ||
乙复印店收费（元） |
|
| … |
（2）设在甲复印店复印收费
元，在乙复印店复印收费
元，分别写出
关于
的函数关系式；
（3）当
时，顾客在哪家复印店复印花费少？请说明理由.
