题目内容
【题目】一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.
(1)求证:M与其“友谊数”的差能被15整除;
(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值.
【答案】
(1)解:由题意可得,
设M为100a+10b+c,则它的友谊数为:100b+10a+c,
(100a+10b+c)﹣(100b+10a+c)
=100a+10b+c﹣100b﹣10a﹣c
=100(a﹣b)+10(b﹣a)
=90(a﹣b),
∵ ![]() ,
,
∴M与其“友谊数”的差能被15整除
(2)解:由题意可得,
N=2×100+10a+b=200+10a+b,
N的团结数是:10×2+a+10a+2+10×2+b+10×b+2+10a+b+10b+a=22a+22b+44,
∴22a+22b+44﹣(200+10a+b)=24,
解得, ![]() 或
或 ![]() ,
,
即N是284或218
【解析】(1)设出字母,表示出这个三位数,按照新定义,表示出友谊数,作差,得出差的代数式,很容易看出能被15整除;(2)用a、b的代数式表示这个三位数,表示出团结数,由已知构建方程,求出a、b.
【考点精析】本题主要考查了用字母表示数的相关知识点,需要掌握单独一个数或者一个字母也是代数式才能正确解答此题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某公司有2位股东,20名工人、从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示.
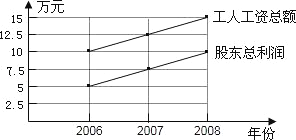
(1)填写下表:
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 | 5000 | ||
股东的平均利润/元 | 25000 |
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?