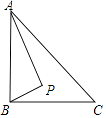题目内容
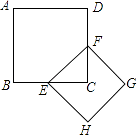
【题目】如图,∠ECF=90°,线段 AB 的端点分别在 CE 和 CF 上,BD 平分∠CBA,并与∠CAB 的外角平分线 AG 所在的直线交于一点 D.
(1)∠D 与∠C 有怎样的数量关系?(直接写出关系及大小)
(2)点 A 在射线 CE 上运动,(不与点 C 重合)时,其它条件不变,(1)中结论还成立吗?说说你的理由.

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据角平分线的性质、外角的性质、三角形内角和定理整理即可得出答案;
(2)根据(1)中结论即可推理得出答案.
(1)∠C=2∠D 即:∠D=45°.
∵BD平分∠CBA,AG平分∠EAB,∴∠EAB=2∠GAB,∠ABC=2∠DBA.
∵∠CAB=180°﹣2∠GAB,∠BAC+∠ABC=90°,即180°﹣2∠GAB+2∠DBA=90°,整理得出∠GAB﹣∠DBA=45°,∴∠D![]() ∠C=45°;
∠C=45°;
(2)当A在射线CE上运动(不与点C重合)时,其它条件不变,(1)中结论还成立.
∵∠CAB+∠ABC=∠C=90°,不论A在CE上如何运动,只要不与C点重合,这个关系式都是不变的,整理这个式子:∠CAB=180°﹣2∠GAB,∠ABC=2∠DBA,得:180°﹣2∠GAB+2∠DBA=90°,整理得:∠GAB﹣∠DBA=45度,恒定不变,即:∠D=45°的结论不变,∴∠C=2∠D恒成立.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目