题目内容
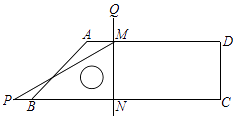
【题目】如图,点A、B的坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.
根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,求t的值;
(2)当t=4时,求S的值;
(3)直接写出S与t的函数关系式(不必写出解题过程);
(4)若S=12,则t= .
【答案】
(1)
解:由题意可得∠BCD=∠BOA=90°,∠CBD=∠OBA,
∴△BCD∽△BOA,
∴ ![]()
而 ![]() ,
,
则 ![]() ,
,
解得 ![]() ,
,
∴当点D在直线AB上时, ![]() .
.
(2)
解:当t=4时,点E与A重合,设CD与AB交于点F,
则由△CBF∽△OBA得 ![]() ,
,
即 ![]() ,
,
解得CF=3,
∴ ![]() .
.
(3)
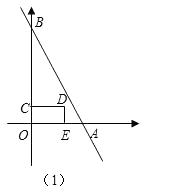
解:①当 ![]() 时,
时, ![]()
②当 ![]() 时,
时, ![]()
③当4<t≤16时, ![]()
分析:①当 ![]() 时,如图(1),
时,如图(1),
②当 ![]() 时,如图(2),
时,如图(2),
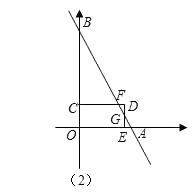
∵A(4,0),B(0,8),∴直线AB的解析式为y=﹣2x+8,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]()
③当4<t≤16时,如图(3)
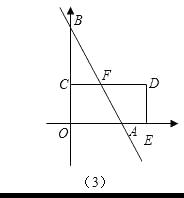
∵CD∥OA,∴△BCF∽△BOA,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]()
(4)8
【解析】分析:由题意可知把S=12代入 ![]() 中,
中, ![]() ,
,
整理,得t2﹣32t+192=0,
解得t1=8,t2=24>16(舍去),
∴当S=12时,t=8.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目