题目内容
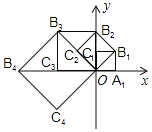
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推……则正方形OB2019B2020C2020的顶点B2020的坐标是 _____.
【答案】![]()
【解析】
首先先求出B1、B2、B3、B4、B5、B6、B7、B8、B9、B10的坐标,找出这些坐标之间的规律,然后根据规律计算出点B2020的坐标.
∵正方形OA1B1C1的边长为1,
∴OB1=![]()
∴OB2=2
∴B2(0,2),
同理可知B3(-2,2),B4(-4,0),B5(-4,-4),B6(0,-8),B7(8,-8),
B9(16,16),B10(0,32).
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标的符号相同,每次正方形的边长变为原来的![]() 倍,
倍,
∵2020÷8=2524,
∴B8n+4(-24k+2,0),
∴B2018(-22010,0).
故答案为:(-22010,0).

练习册系列答案
相关题目