Question

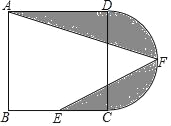
【题目】如图，长方形中∥，边，．将此长方形沿折叠，使点与点重合，点落在点处．

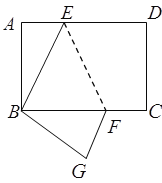
（1）试判断的形状，并说明理由；

（2）求的面积．

Answer 1

【答案】（1）是等腰三角形；（2）10

【解析】

试题（1）根据翻折不变性和平行线的性质得到两个相等的角，根据等角对等边即可判断△BEF是等腰三角形；

（2）根据翻折的性质可得BE=DE，BG=CD，∠EBG=∠ADC=90°，设BE=DE=x，表示出AE=8-x，然后在Rt△ABE中，利用勾股定理列出方程求出x的值，即为BE的值，再根据同角的余角相等求出∠ABE=∠GBF，然后利用“角边角”证明△ABE和△GBF全等，根据全等三角形对应边相等可得BF=BE，再根据三角形的面积公式列式计算即可得解．

试题解析：解：（1）△BEF是等腰三角形．

∵ED∥FC，

∴∠DEF=∠BFE，

根据翻折不变性得到∠DEF=∠BEF，

故∠BEF=∠BFE．

∴BE=BF．

△BEF是等腰三角形；

（2）∵矩形ABCD沿EF折叠点B与点D重合，

∴BE=DE，BG=CD，∠EBG=∠ADC=90°，∠G=∠C=90°，

∵AB=CD，

∴AB=BG，

设BE=DE=x，则AE=AB-DE=8-x，

在Rt△ABE中，AB2+AE2=BE2，

即42+2=x2，

解得x=5，

∴BE=5，

∵∠ABE+∠EBF=∠ABC=90°，

∠GBF+∠EBF=∠EBG=90°，

∴∠ABE=∠GBF，

在△ABE和△MBF中，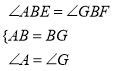

∴△ABE≌△GBF（ASA），

∴BF=BE=5，

∴△EBF的面积=×5×4=10．