ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŅŃÖŖĖıߊĪABCDĪŖ¾ŲŠĪ£¬¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO£¬AD£½AO£®µćE”¢FĪŖ¾ŲŠĪ±ßÉĻµÄĮ½øö¶Æµć£¬ĒŅ”ĻEOF£½60”ć£®
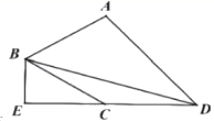
£Ø1£©ČēĶ¼1£¬µ±µćE”¢F·Ö±šĪ»ÓŚAB”¢AD±ßÉĻŹ±£¬Čō”ĻOEB£½75”ć£¬ĒóÖ¤£ŗDF£½AE£»
£Ø2£©ČēĶ¼2£¬µ±µćE”¢FĶ¬Ź±Ī»ÓŚAB±ßÉĻŹ±£¬Čō”ĻOFB£½75”ć£¬ŹŌĖµĆ÷AFÓėBEµÄŹżĮæ¹ŲĻµ£»
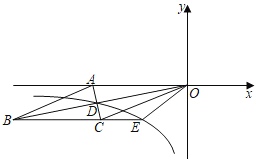
£Ø3£©ČēĶ¼3£¬µ±µćE”¢FĶ¬Ź±ŌŚAB±ßÉĻŌĖ¶ÆŹ±£¬½«”÷OEFŃŲOEĖłŌŚÖ±Ļß·ÕŪÖĮ”÷OEP£¬Č”Ļ߶ĪCBµÄÖŠµćQ£®Į¬½ÓPQ£¬ČōAD£½2a£Øa£¾0£©£¬Ōņµ±PQ×ī¶ĢŹ±£¬ĒóPFÖ®³¤£®

”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©AF£½2BE£¬¼ū½āĪö£»£Ø3£©![]() a
a
”¾½āĪö”æ
£Ø1£©ČēĶ¼1ÖŠ£¬ŌŚODÉĻČ”Ņ»µćK£¬Ź¹µĆOK£½OE£¬Į¬½ÓDK£®Ļė°ģ·ØÖ¤Ć÷DK£½AE£¬DF£½DK¼“æɽā¾öĪŹĢā£®
£Ø2£©ČēĶ¼2ÖŠ£¬½«”÷OAFČʵćOÄꏱÕėŠż×Ŗ120”ćµĆµ½”÷OBJ£¬Į¬½ÓJE£®Ļė°ģ·ØÖ¤Ć÷”ĻJEB£½90”ć£¬”ĻEJB£½30”ćæÉµĆ½įĀŪ£®
£Ø3£©ČēĶ¼3ÖŠ£¬Į¬½ÓBP£®Ö¤Ć÷”÷OAF”Õ”÷OBP£ØSAS£©£¬ĶĘ³ö”ĻPBC£½30”ć£¬ČēĶ¼3©1ÖŠ£¬µ±QP”ĶPBŹ±£¬PQµÄÖµ×īŠ”£¬×÷FH”ĶOAÓŚH£¬OM”ĶPFÓŚM£®½āÖ±½ĒČż½ĒŠĪĒó³öFM¼“æɽā¾öĪŹĢā£®
£Ø1£©Ö¤Ć÷£ŗČēĶ¼1ÖŠ£¬ŌŚODÉĻČ”Ņ»µćK£¬Ź¹µĆOK£½OE£¬Į¬½ÓDK£®
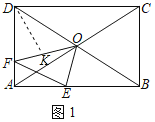
”ßĖıߊĪABCDŹĒ¾ŲŠĪ£¬
”ąOD£½OA£¬”ĻDAB£½90”ć£¬
”ßAD£½AO£¬
”ąAD£½AO£½OD£¬
”ą”÷OADŹĒµČ±ßČż½ĒŠĪ£¬
”ą”ĻDOA£½”ĻEOF£½”ĻDAO£½”ĻADO£½60”ć£¬
”ą”ĻDOK£½”ĻAOE£¬”ĻOAE£½90”ć©60”ć£½30”ć£¬
”ßOD£½OA£¬OK£½OE£¬
”ą”÷DOK”Õ”÷AOE£ØSAS£©£¬
”ąDK£½AE£¬”ĻODK£½”ĻOAE£½30”ć£¬
”ßOA£½OB£¬
”ą”ĻOAB£½”ĻOBA£½30”ć£¬
”ß”ĻOEB£½75”ć£¬
”ą”ĻOEB£½”ĻBOE£½75”ć£¬
”ß”ĻEOF£½60”ć£¬
”ą”ĻDOK£½180”ć©75”ć©60”ć£½45”ć£¬
”ą”ĻDFO£½180”ć©60”ć©45”ć£½75”ć£¬”ĻDKO£½”ĻODK+”ĻDOK£½75”ć£¬
”ą”ĻDFK£½”ĻDKF£½75”ć£¬
”ąDF£½DK£¬
”ąDF£½AE£®
£Ø2£©½ā£ŗ½įĀŪ£ŗAF£½2BE£®
ĄķÓÉ£ŗČēĶ¼2ÖŠ£¬½«”÷OAFČʵćOÄꏱÕėŠż×Ŗ120”ćµĆµ½”÷OBJ£¬Į¬½ÓJE£®

”ß”ĻAOB£½120”ć£¬”ĻEOF£½60”ć£¬
”ą”ĻBOJ+”ĻBOE£½”ĻAOF+”ĻBOE£½60”ć£¬
”ą”ĻEOJ£½”ĻEOF£¬
”ßOF£½OJ£¬OE£½OE£¬
”ą”÷EOF”Õ”÷EOJ£ØSAS£©£¬
”ą”ĻOEF£½”ĻOEJ£¬
”ß”ĻOFB£½75”ć£¬”ĻOBF£½30”ć£¬
”ą”ĻBOF£½75”ć£¬
”ą”ĻBOE£½75”ć©60”ć£½15”ć£¬
”ą”ĻFEO£½”ĻBOE+”ĻOBE£½45”ć£¬
”ą”ĻOEF£½”ĻOEJ£½45”ć£¬
”ą”ĻJEB£½”ĻJEF£½90”ć£¬
”ß”ĻOBJ£½”ĻOAF£½30”ć£¬”ĻOBE£½30”ć£¬
”ą”ĻEBJ£½60”ć£¬
”ą”ĻEJB£½90”ć©60”ć£½30”ć£¬
”ąBJ£½2BE£¬
”ßAF£½BJ£¬
”ąAF£½2BE£®
£Ø3£©½ā£ŗČēĶ¼3ÖŠ£¬Į¬½ÓBP£®
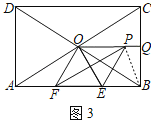
ÓÉ·ÕŪæÉÖŖ£ŗOE£½OP£¬”ĻEOF£½”ĻEOP£½60”ć£¬
”ą”ĻFOP£½”ĻAOB£½120”ć£¬
”ą”ĻAOF£½”ĻBOP£¬
”ßOA£½OB£¬
”ą”÷OAF”Õ”÷OBP£ØSAS£©£¬
”ą”ĻOBP£½”ĻOAF£½30”ć£¬AF£½BP£¬
”ß”ĻOBC£½60”ć£¬
”ą”ĻPBC£½30”ć£¬
ČēĶ¼3©1ÖŠ£¬µ±QP”ĶPBŹ±£¬PQµÄÖµ×īŠ”£¬×÷FH”ĶOAÓŚH£¬OM”ĶPFÓŚM£®

ŌŚRt”÷PQBÖŠ£¬”ß”ĻQPB£½90”ć£¬”ĻPBQ£½30”ć£¬BQ£½![]() BC£½
BC£½![]() AD£½a£¬
AD£½a£¬
”ąPB£½AF£½BQcos30”ć£½![]() a£¬
a£¬
ŌŚRt”÷AFHÖŠ£¬ŌņÓŠAH£½AFcos30”ć£½![]() a£¬FH£½
a£¬FH£½![]() AF£½
AF£½![]() £¬
£¬
”ąOH£½OA©AH£½2a©![]() a£½
a£½![]() £¬
£¬
”ąOF£½ £¬
£¬
”ßOF£½OP£¬OM”ĶPF£¬
”ąFM£½MP£½OFcos30”ć£½![]() £¬
£¬
”ąFP£½2FM£½![]() a£®
a£®

 ĆææĪ±ŲĮ·ĻµĮŠ“š°ø
ĆææĪ±ŲĮ·ĻµĮŠ“š°ø