Question

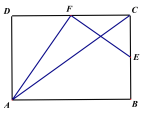
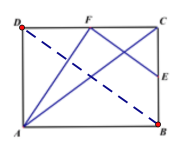
【题目】如图，E、F分别是矩形ABCD的边BC、CD的中点，连接AC、AF、EF，若AF⊥EF，AC=，则AB的长为_____．

Answer 1

【答案】2

【解析】连接BD，由E、F分别BC、CD的中点，得EF=,设AB=x,则DF=CF=，由勾股定理得，CE2+CF2=EF2 ,求得，AD=2CE=，再证△ADF∽△FCE,得 ，即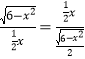，化简可得.

连接BD，

因为，四边形ABCD是矩形，

所以，BD=AC=,

因为，E、F分别BC、CD的中点，

所以，EF=,

设AB=x,则DF=CF=，

由勾股定理得，CE2+CF2=EF2 ,

即 ，

，

所以，AD=2CE=，

因为，EF⊥AF,

所以，∠AFE=90o

所以，∠AFD+∠CFE=90o

又因为，∠CEF+∠CFE=90o

所以，∠AFD=∠CEF

又∠ADF=∠FCE==90o

所以，△ADF∽△FCE

所以,

所以，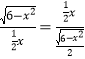

解得x=2.

即AB=2.

故答案为：2