题目内容
【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG. 
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
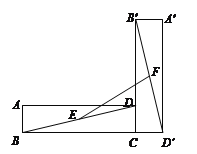
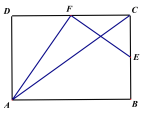
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
【答案】
(1)证明:如图①,作∠GAH=∠EAB交GE于点H.
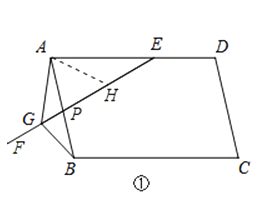
∴∠GAB=∠HAE.
∵∠EAB=∠EGB,∠APE=∠BPG,
∴∠ABG=∠AEH.
在△ABG和△AEH中,
 ,
,
∴△ABG≌△AEH(ASA).
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG;
(2)EG= ![]() AG﹣BG.
AG﹣BG.
如图②,作∠GAH=∠EAB交GE于点H.
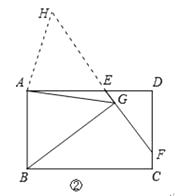
∴∠GAB=∠HAE.
∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH=180°.
∴∠ABG=∠AEH.
∵又AB=AE,
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴ ![]() AG=HG.
AG=HG.
∴EG= ![]() AG﹣BG.
AG﹣BG.
【解析】(1)首先作∠GAH=∠EAB交GE于点H,易证得△ABG≌△AEH,又由∠EAB=60°,可证得△AGH是等边三角形,继而证得结论;(2)首先作∠GAH=∠EAB交GE于点H,易证得△ABG≌△AEH,继而可得△AGH是等腰直角三角形,则可求得答案.
【考点精析】利用平行四边形的性质对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目