题目内容
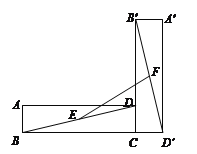
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 . 
【答案】3
【解析】解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1, ∴∠CAB=30°,故AB=2,
∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=2,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=1,
∴AA′=1+2=3,
故答案为3.
利用直角三角形的性质得出AB=2,再利用旋转的性质以及三角形外角的性质得出AB′=1,进而得出答案.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目