题目内容
【题目】如图,海边有两个灯塔A,B.即将靠岸的轮船得到信息:海里有一个以AB为弦的弓形暗礁区域,要求轮船在行驶过程中,对两灯塔的张角不能超过![]() .当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于
.当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于![]() .
.

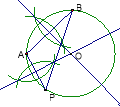
(1)请用直尺和圆规在图中作出△APB的外接圆 (作出图形,不写作法,保留痕迹);
(2)若此时轮船到B的距离PB为700米,已知AB=500米,求出此时轮船到A的距离.
【答案】(1)、答案见解析;(2)、300![]() 或400
或400![]()
【解析】
试题分析:(1)、根据外接圆的画法得出图形;(2)、过点B作BH⊥AP,根据∠P=45°得到BH=PH,设BH=PH=x,则AH=700-x,根据Rt△BAH的勾股定理求出x的值,然后得出BP的长度.
试题解析:(1)、如图:⊙O就是所求作的圆
、如图,过B作BH⊥AP,
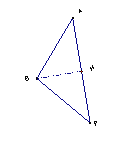
在Rt△BPH中, ∵∠P=45, ∴BH=PH
设BH=PH=x,则AH=700-x 在Rt△BAH中,![]() 解得:x=300或x=400
解得:x=300或x=400
∴BP=300![]() 米或BP=400
米或BP=400![]() 米.
米.
答:轮船距离B有300![]() 或400
或400![]() 米.
米.

练习册系列答案
相关题目