��Ŀ����
����������12�֣���ͼ�ף��ֱ��������˴����ڵ�������?OABC��CDEF�ı�OC��OA����ֱ��Ϊx�ᡢy�Ὠ��ƽ��ֱ������ϵ��O��C��F������x���������ϣ�.����P��A��B��E����(Բ����x����)��������y=14x2+bx+c����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1.

1.��1����B�����ꣻ
2.��2����֤��ME�ǡ�P�����ߣ�
3.��3����ֱ��AC�������߶Գ��ύ��N��Q���Ǵ˶Գ����ϲ���N���غϵ�һ���㣬�����ACQ�ܳ�����Сֵ��
����FQ��t��S��ACQ��S��ֱ��д��S��t֮��ĺ�����ϵʽ.
1.��1����ͼ�ף�����PE��PB����PC=n��
��������CDEF�����Ϊ1��
��CD=CF=1��
����Բ�������εĶԳ���֪��OP=PC=n��
��BC=2PC=2n��
�߶�PB=PE��
��PB2=BC2+PC2=4n2+n2=5n2��PE2=PF2+EF2=��n+1��2+1��
��5n2=��n+1��2+1��
��ã�n=1��n=- 12����ȥ����
��BC=OC=2��
��B��������2��2����
2.��2����ͼ�ף��ɣ�1��֪A��0��2����C��2��0����
��A��C���������ϣ�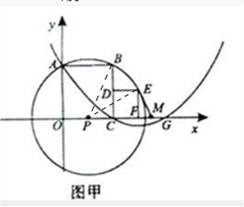
\�� {c=214��4+2b+c=0��
��ã� {c=2b=-32��
�������ߵĽ���ʽΪ��y= 14x2- 32x+2= 14��x-3��2- 14��
�������ߵĶԳ���Ϊx=3����EF����ֱ�ߣ�
��C��G����ֱ��x=3�Գƣ�
��CF=FG=1��
��MF= 12FG= 12��
��Rt��PEF��Rt��EMF��
��EFM=��EFP��
�� FMEF=121=12�� EFPF=12��
�� FMEF=EFPF��
���PEF�ס�EMF��
����EPF=��FEM��
���PEM=��PEF+��FEM=��PEF+��EPF=90�㣬
��ME�ǡ�P�����ߣ�
3.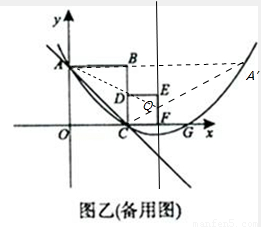
��3������ͼ�ң��ӳ�AB����������A�䣬��CA�佻�Գ���x=3��Q����AQ��
����AQ=A��Q��
���ACQ�ܳ�����СֵΪAC+A��C�ij���
��A��A�����ֱ��x=3�Գƣ�
��A��0��2����A�䣨6��2����
��A��C=��6-2��2+22=2 5����AC=22+22=2 2��
���ACQ�ܳ�����СֵΪ2 2+2 5��
�ڵ�Q����F���Ϸ�ʱ��S=t+1��
��Q�����߶�FN��ʱ��S=1-t��
��Q����N���·�ʱ��S=t-1��
����������

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�����������12�֣�
��ͼ�� �Ķ���A��B�ڶ��κ���
�Ķ���A��B�ڶ��κ��� ��ͼ���ϣ��ֵ�A��B[���ֱ���
��ͼ���ϣ��ֵ�A��B[���ֱ��� ���
��� ���ϣ�
���ϣ� ��ABO��
��ABO�� ��
��

1.��1����˶��κ����Ľ���ʽ����4�֣�
2.
|
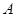 ��
�� ��
�� ����������ͼ���ڵ�
����������ͼ���ڵ� ��
��
�� ����������ͼ���ϣ���
����������ͼ���ϣ��� ��
�� ����ʱ�����
����ʱ����� �����꣮��8�֣�
�����꣮��8�֣�

 �ij���
�ij���
 ��x�ύ��A��C���㣬��y�ύ��B�㣬��ֱ��
��x�ύ��A��C���㣬��y�ύ��B�㣬��ֱ�� ����A��D���㡣
����A��D���㡣 ����ͼ1����������ֱ��Χ�������ڣ�ͼ����Ӱ���֣����߽磩�ĸ����Ƕ��٣�
����ͼ1����������ֱ��Χ�������ڣ�ͼ����Ӱ���֣����߽磩�ĸ����Ƕ��٣�

 ��
�� ��
�� ������M��ÿ��1����λ�����ٶȣ��ӵ�A���߶�AB���B�˶���ͬʱ��P����ͬ���ٶȣ��ӵ�C������C-D-A���A�˶�������M�����Bʱ������ͬʱֹͣ�˶�������M��ֱ��l��AD�����߶�CD�Ľ���ΪE��������A-C-B�Ľ���ΪQ����M�˶���ʱ��Ϊt���룩��
������M��ÿ��1����λ�����ٶȣ��ӵ�A���߶�AB���B�˶���ͬʱ��P����ͬ���ٶȣ��ӵ�C������C-D-A���A�˶�������M�����Bʱ������ͬʱֹͣ�˶�������M��ֱ��l��AD�����߶�CD�Ľ���ΪE��������A-C-B�Ľ���ΪQ����M�˶���ʱ��Ϊt���룩��
 ʱ�����߶�
ʱ�����߶� �ij���
�ij��� �Ƿ�Ϊ��ֵ�����ǣ����������ֵ�������ǣ���˵�����ɣ�
�Ƿ�Ϊ��ֵ�����ǣ����������ֵ�������ǣ���˵�����ɣ�