��Ŀ����
����Ŀ����1���Ķ����⣺

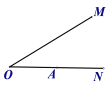
��ͼ�٣�����ABC�У���AB=5��AC=3����BC���ϵ�����AD��ȡֵ��Χ.
�����������������·������ӳ�AD����EʹDE=AD��������BE(����ACD���ŵ�D��ʱ����ת180���õ���EBD)����AB��AC��2AD��������ABE�У��������������ߵĹ�ϵ�����ж�.����AD��ȡֵ��Χ��___________��
(2)������: ��ͼ�ڣ�����ABC��,D��BC���ϵ��е�,DE��DF�ڵ�D,DE��AB�ڵ�E,DF��AC�ڵ�F,����EF,��֤:BE+CF��EF��
(3)������չ:��ͼ��,���ı���ABCD��,��B+��D=180��,CB=CD,��CΪ��������ECF,ʹ�ýǵ����߷ֱ�AB,AD��E��F����,����EF,��EF=BE+DF����̽����ECF���A֮���������ϵ,������֤��.
���𰸡���1��1��AD��4����2��֤������������3����A+2��ECF=180�������ɼ�����.
��������
��1���ӳ�AD��E��ʹDE=AD������BE��֤��ADC�ա�EDB���Ƴ�EB=AC�����������ε����߹�ϵ������ɣ�
��2��������ASA�ж���BGD�ա�CFD���Ӷ��ó�BG=CF��������ȫ�ȵ����ʿɵ�GD=FD������DE��GF���Ӷ��ó�EG=EF�����ߺʹ��ڵ����ߴӶ��ó�BE+CF��EF��
��3���ӳ�EB��G��ʹBG=DF������CG��ͨ��SAS֤����CDF����CBG���õ�CG=CF����BCG=��DCF����֤����CEF����CEG���õ���ECF=��EDG������A+��BCD=180����ͨ�������������ɵõ���A+2��ECF=180��.
��1���ӳ�AD��E��ʹAD=DE������BE��
��AD�ǡ�ABC�����ߣ�
��BD=CD��
�ڡ�ADC���EDB�У�
 ��
��
���ADC�ա�EDB��SAS����
��EB=AC��
��AB=5��AC=3��
���������ε����߹�ϵ�ã�AB-AC��AE��AC+AB��
��2��AE��8��
��AE=2AD
��1��AD��4��
����BC���ϵ�����AD��ȡֵ��Χ1��AD��4��
�ʴ�Ϊ��1��AD��4��
��2������B��BG��AC��FD���ӳ�����G������EG��

���DBG=��DCF��
��DΪBC���е㣬
��BD=CD��
�֡ߡ�BDG=��CDF��
���BGD�ա�CFD��ASA����
��GD=FD��BG=CF��
�֡�DE��DF��
��EG=EF����ֱƽ���ߵ��߶ζ˵�ľ�����ȣ���
���ڡ�EBG�У�BE+BG��EG��
��BE+CF��EF��
��3����A+2��ECF=180�����������£�
�ӳ�EB��G��ʹBG=DF������CG��
����D+��ABC=180������ABC+��CBG=180����
���D=��CBG��
�֡�CD=CB��DF=BG��
���CDF����CBG��
��CF=CG����DCF=��BCG��
��EF=DF+BE��EG=BE+BG��DF=BG��
��EF=EG��
����EC=EC��
����CEF�ա�CEG��
���ECF=��ECG��
�ߡ�BCD=��DCF+��BCF��
���BCD=��BCF+��BCG=��FCG=��ECF+��ECG=2��ECF��
�ߡ�D+��A+��ABC+��BCD=360������D+��ABC=180����
���A+��BCD=180����
����A+2��ECF=180��.