题目内容
【题目】已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.
(1)如图1,求证:DE=DF; 
(2)如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形; 
(3)如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2 ![]() ,BE=4
,BE=4 ![]() ,求DH的长.
,求DH的长. 
【答案】
(1)证明:如图1中,连接BC.
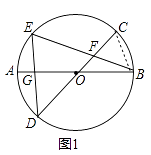
∵OB=OC,
∴∠C=∠OBC=∠E,
∵GO=GD,
∴∠D=∠GOD=∠EBC=∠BOC,
∵∠OBC=∠EBC+∠EBA,∠EFD=∠BOC+∠EBA,
∵∠EBC=∠BOC,
∴∠OBC=∠EFD=∠E,
∴DE=DF.
(2)证明:如图2中,连接AD、DK、BC.
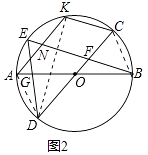
∵AK∥CD,
∴∠AKD=∠KDC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴∠ADC=∠KCD,
∵∠ADO=∠OBC=∠OCB=∠E=∠EFD,
∴∠KCD=∠EFD,
∴KC∥FN,∵KN∥FC,
∴四边形KNFC是平行四边形.
(3)解:如图3中,作ON⊥BE于N,HK⊥CD于K,连接EO.
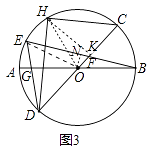
∵ON⊥EB,
∴EN=BN=2 ![]() ,
,
∵∠CDH=3∠EDH,
设∠EDH=x,则∠CDH=3x,∠OHD=∠ODH=3x,∠HOC=∠D+∠OHD=6x,∠GOD=∠GDO=∠BOC=4x,∠HOB=∠HOC+∠BOC=10x,∠EOC=∠ODE+∠OED=8x,∠EOB=∠EOC+∠BOC=12x,
∵∠BON=∠EON=6x,
∴∠HOK=∠BON=6x,
在△OHK和△OBN中,
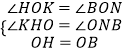 ,
,
∴△OHK≌△OBN,
∴HK=BN=2 ![]() ,
,
在Rt△CHK中,CK= ![]() =
= ![]() =4,
=4,
∵CD是直径,
∴∠CHD=∠CKH=90°,
∵∠C=∠C,
∴△CKH∽△CHD,
∴ ![]() =
= ![]() ,
,
∴DH= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)如图1中,连接BC.欲证明DE=DF,只要证明∠E=∠EFD.(2)如图2中,连接AD、DK、BC.首先证明∠ADC=∠KCD,再证明∠EFD=∠ADC,即可推出∠EFD=∠KCD,推出KC∥FN,由此即可解决问题.(3)如图3中,作ON⊥BE于N,HK⊥CD于K,连接EO.想办法证明△OHK≌△OBN,推出HK=BN=2 ![]() ,再证明△CKH∽△CHD,得
,再证明△CKH∽△CHD,得 ![]() =
= ![]() ,利用勾股定理求出KC即可解决问题.
,利用勾股定理求出KC即可解决问题.

【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元. 经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元) | … | 70 | 90 | … |
销售量y(件) | … | 3000 | 1000 | … |
(利润=(售价﹣成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40000元?