题目内容
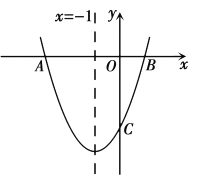
【题目】已知二次函数
，一次函数
，
有下列结论：
①当
时，
随
的增大而减小；
②二次函数的图象与轴交点的坐标为
和
；
③当
时，
；
④在实数范围内，对于的同一个值，这两个函数所对应的函数值
均成立，则
.
其中，正确结论的个数是（ ）
A.0B.1C.2D.3
【答案】C
【解析】
根据“二次函数”和“一次函数”可知，本题考察二次函数的解析式和一次函数的图像与性质知识点，根据二次函数和一次函数性质，运用图像法，代入法，求根公式等进行求解．
①二次函数
的对称轴为
，因为m的正负性不确定，所以
与
的关系无法确定，故①错误；
②把
代入，解得
，
，所以图象与轴交点的坐标为
和
，故②正确；
③当
时，二次函数为
，将一次函数与二次函数列方程
，解得
，，所以当
，
，故③错误；
④
对于任意都成立，即
，
有且仅有一个解
则
，
，故④正确．
故选C．
练习册系列答案
智能训练练测考系列答案
相关题目
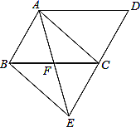
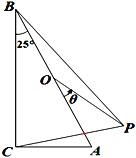
【题目】如图，在△ABC中，∠ACB=90°，∠ABC=25°，O为AB的中点. 将OA绕点O逆时针旋转θ °至OP（0<θ<180），当△BCP恰为轴对称图形时，θ的值为_____________．
【题目】某游泳馆推出了两种收费方式．
方式一：顾客先购买会员卡，每张会员卡200元，仅限本人一年内使用，凭卡游泳，每次游泳再付费30元．
方式二：顾客不购买会员卡，每次游泳付费40元．
设小亮在一年内来此游泳馆游泳的次数为
次（为正整数）．
（1）根据题意，填写下表：
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用（元） | 350 | 650 | … | ||
方式二的总费用（元） | 200 | 400 | … |
（2）若小亮计划今年游泳的总费用为2000元，选择哪种付费方式，他游泳的次数比较多；
（3）当
时，小亮选择哪种付费方式更合算．并说明理由.
