ЬтФПФкШн
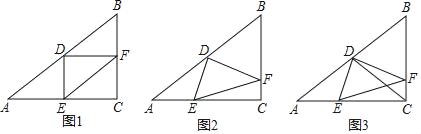
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=8ЃЌcosA=![]() ЃЌDЪЧABБпЕФжаЕуЃЌEЪЧACБпЩЯвЛЕуЃЌСЊНсDEЃЌЙ§ЕуDзїDFЁЭDEНЛBCБпгкЕуFЃЌСЊНсEFЃЎ
ЃЌDЪЧABБпЕФжаЕуЃЌEЪЧACБпЩЯвЛЕуЃЌСЊНсDEЃЌЙ§ЕуDзїDFЁЭDEНЛBCБпгкЕуFЃЌСЊНсEFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБDEЁЭACЪБЃЌЧѓEFЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкACБпЩЯвЦЖЏЪБЃЌЁЯDFEЕФе§ЧажЕЪЧЗёЛсЗЂЩњБфЛЏЃЌШчЙћБфЛЏЧыЫЕГіБфЛЏЧщПіЃЛШчЙћБЃГжВЛБфЃЌЧыЧѓГіЁЯDFEЕФе§ЧажЕЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌСЊНсCDНЛEFгкЕуQЃЌЕБЁїCQFЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіBFЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉEF=5ЃЛЃЈ2ЃЉВЛБфЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉBFЕФГЄЮЊ3Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩcosA=![]() ЃЌИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхПЩЧѓПЩЧѓAC=8ЃЌAE=4ЃЌдкRtЁїEDFжаЃЌгЩЙДЙЩЖЈРэЧѓГіDE=3ЃЌдкRtЁїAEDжаЃЌгЩЙДЙЩЖЈРэЧѓГіEFЕФГЄЃЛ
ЃЌИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхПЩЧѓПЩЧѓAC=8ЃЌAE=4ЃЌдкRtЁїEDFжаЃЌгЩЙДЙЩЖЈРэЧѓГіDE=3ЃЌдкRtЁїAEDжаЃЌгЩЙДЙЩЖЈРэЧѓГіEFЕФГЄЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDHЁЭACЃЌDGЁЭBCЃЌДЙзуЗжБ№ЮЊЕуHЁЂGЃЌгЩЃЈ1ЃЉПЩЕУDH=3ЃЌDG=4ЃЌдйжЄЁїEDHЁзЁїFDGЃЌЕУЕН![]() ,ШЛКѓИљОне§ЧаЖЈвхЧѓНтЃЛ
,ШЛКѓИљОне§ЧаЖЈвхЧѓНтЃЛ
ЃЈ3ЃЉЗжQF=QCЃЌFQ=FCЃЌCF=CQШ§жжЧщПіЧѓНт.
НтЃКЃЈ1ЃЉЁпЁЯACB=90ЁуЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
ЁпAC=8ЃЌ
ЁрAB=10ЃЌ
ЁпDЪЧABБпЕФжаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпDEЁЭACЃЌ
ЁрЁЯDEA=ЁЯDEC=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=4ЃЌ
ЁрCE=8Љ4=4ЃЌ
ЁпдкRtЁїAEDжаЃЌAE2+DE2=AD2ЃЌ
ЁрDE=3ЃЌ
ЁпDFЁЭDEЃЌ
ЁрЁЯFDE=90ЁуЃЌ
гжЁпЁЯACB=90ЁуЃЌ
ЁрЫФБпаЮDECFЪЧОиаЮЃЌ
ЁрDF=EC=4ЃЌ
ЁпдкRtЁїEDFжаЃЌDF2+DE2=EF2ЃЌ
ЁрEF=5
ЃЈ2ЃЉВЛБф
ШчЭМ2ЃЌ
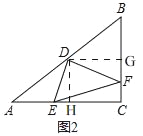
Й§ЕуDзїDHЁЭACЃЌDGЁЭBCЃЌДЙзуЗжБ№ЮЊЕуHЁЂGЃЌ
гЩЃЈ1ЃЉПЩЕУDH=3ЃЌDG=4ЃЌ
ЁпDHЁЭACЃЌDGЁЭBCЃЌ
ЁрЁЯDHC=ЁЯDGC=90Ёу
гжЁпЁЯACB=90ЁуЃЌ
ЁрЫФБпаЮDHCGЪЧОиаЮЃЌ
ЁрЁЯHDG=90ЁуЃЌ
ЁпЁЯFDE=90ЁуЃЌ
ЁрЁЯHDGЉЁЯHDF=ЁЯEDFЉЁЯHDFЃЌ
МДЁЯEDH=ЁЯFDGЃЌ
гжЁпЁЯDHE=ЁЯDGF=90Ёу
ЁрЁїEDHЁзЁїFDGЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯFDE=90ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈ3ЃЉЂйЕБQF=QCЪБЃЌ
ЁрЁЯQFC=ЁЯQCFЃЌ
ЁпЁЯEDF+ЁЯECF=180ЁуЃЌ
ЁрЕуDЃЌEЃЌCЃЌFЫФЕуЙВдВЃЌ
ЁрЁЯECQ=ЁЯDFEЃЌЁЯDFE+ЁЯQFC=ЁЯECQ+ЁЯQCF=ЁЯACB=90ЁуЃЌ
МДЁЯDFC=90ЁуЃЌ
гжЁпЁЯACB=90ЁуЃЌDЪЧABЕФжаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂкЕБFQ=FCЪБЃЌ
ЁрЁЯBCD=ЁЯCQFЃЌ
ЁпЕуDЪЧABЕФжаЕуЃЌ
ЁрBD=CD=![]() AB=5ЃЌ
AB=5ЃЌ
ЁрЁЯBDC=ЁЯBCDЃЌ
ЁрЁЯBCD=ЁЯFCQЃЌЁЯBDC=ЁЯCFQЃЌ
ЁрЁїFQCЁзЁїDCBЃЌ
гЩЂйжЊЃЌЕуDЃЌEЃЌCЃЌFЫФЕуЙВдВЃЌ
ЁрЁЯDEF=ЁЯDCFЃЌ
ЁпЁЯDQE=ЁЯFQCЃЌ
ЁрЁїFQCЁзЁїDEQЃЌ
МДЃКЁїFQCЁзЁїDEQЁзЁїDCB
ЁпдкRtЁїEDFжаЃЌ![]() ЃЌ
ЃЌ
ЁрЩшDE=3kЃЌдђDF=4kЃЌEF=5kЃЌ
ЁпЁЯDEF=ЁЯDCF=ЁЯCQF=ЁЯDQEЃЌ
ЁрDE=DQ=3kЃЌ
ЁрCQ=5Љ3kЃЌ
ЁпЁїDEQЁзЁїDCBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁїFQCЁзЁїDCBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂлЕБCF=CQЪБЃЌШчЭМ3ЃЌ
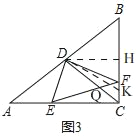
ЁрЁЯBCD=ЁЯCQFЃЌ
гЩЂкжЊЃЌCD=BDЃЌ
ЁрЁЯBDC=ЁЯBCDЃЌ
ЁпЁїEDQЁзЁїBDKЃЌ
дкBCБпЩЯНиШЁBK=BD=5ЃЌЙ§ЕуDзїDHЁЭBCгкHЃЌ
ЁрDH=![]() AC=4ЃЌBH=
AC=4ЃЌBH=![]() BC=3ЃЌгЩЙДЙЩЖЈРэЕУ
BC=3ЃЌгЩЙДЙЩЖЈРэЕУ![]() ЃЌ
ЃЌ
ЭЌЂкЕФЗНЗЈЕУЃЌЁїCFQЁзЁїEDQЃЌ
ЁрЩшDE=3mЃЌдђEQ=3mЃЌEF=5mЃЌ
ЁрFQ=2mЃЌ
ЁпЁїEDQЁзЁїBDKЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрDQ=![]() mЃЌ
mЃЌ
ЁрCQ=FC=5Љ![]() mЃЌ
mЃЌ
ЁпЁїCQFЁзЁїBDKЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр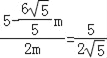 ЃЌ
ЃЌ
НтЕУm=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
МДЃКЁїCQFЪЧЕШбќШ§НЧаЮЪБЃЌBFЕФГЄЮЊ3Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ

 гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ
гЎдкПЮЬУУћЪІПЮЪБМЦЛЎЯЕСаД№АИ ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ
ЬьЬьЯђЩЯПЮЪБЭЌВНбЕСЗЯЕСаД№АИ