题目内容
【题目】如图，AB为⊙O的弦，AB=8，OC⊥AB于点D，交⊙O于点C，且CD=l，求⊙O的半径． 
【答案】解：如图：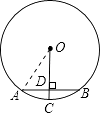 
连接OA，由OC⊥AB于D，得：AD=DB= 
AB=4．
设⊙O的半径为r，在Rt△OAD中，OA2=AD2+OD2
∴r2=（r﹣1）2+42
整理得：2r=17
∴r= 
．
所以圆的半径是 ．
【解析】根据垂径定理得到直角三角形，然后在直角三角形中运用勾股定理计算出半径的长．
【考点精析】根据题目的已知条件，利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
练习册系列答案
相关题目
【题目】某小区开展“节约用水，从我做起”活动，下表是从该小区抽取的10个家庭，8月份比7月份节约用水情况统计：
节水量（m3） | 0.2 | 0.3 | 0.4 | 0.5 |
家庭数（个） | 1 | 2 | 3 | 4 |
那么这10个家庭8月份比7月份的节水量的平均数是（ ）
A.0.5m3
B.0.4m3
C.0.35m3
D.0.3m3
