��Ŀ����
����Ŀ�����壺���һ��ֱ����һ����������ֻ��һ�����㣬������λ��ֱ�ߵ�ͬ�ԣ���֮Ϊֱ�����������У�����ֱ�߽������ߵ����ߣ�ֱ�������ߵ�Ψһ��������е㣮
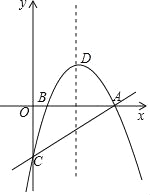
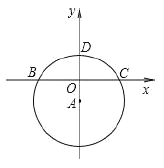
��1����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬�Ե�
Ϊ����ԭ�㣬�Ե�![]() ΪԲ�ģ�5Ϊ�뾶��Բ
ΪԲ�ģ�5Ϊ�뾶��Բ![]() ����
����![]() ��ĸ������ڵ�
��ĸ������ڵ�![]() �������
�������![]() ��Բ
��Բ![]() �����ߵĽ���ʽ��
�����ߵĽ���ʽ��
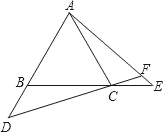
��2����������![]() ��
��![]() ����ֱ��
����ֱ��![]() ��
��![]() �������ڵ�
�������ڵ�![]() ����ֱ�ߵĽ���ʽ��
����ֱ�ߵĽ���ʽ��
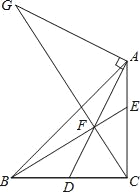
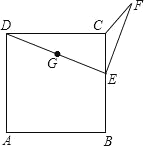
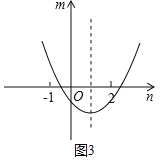
��3��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���У��ҵ�
���У��ҵ�![]() ʱ��
ʱ��![]() ����СֵΪ
����СֵΪ![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ����2��
����2��![]() ����3��1��
����3��1��![]()
��������
��1������![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��![]() ���ߣ�����
���ߣ�����![]() ���ټӹ�����
���ټӹ�����![]() ����֤
����֤![]() ���ɶ�Ӧ�߳ɱ�������
���ɶ�Ӧ�߳ɱ�������![]() �ij��������õ�
�ij��������õ�![]() ���꣬������ֱ��
���꣬������ֱ��![]() ����ʽ��
����ʽ��
��2���ֱ�ѵ�![]() ���������ߺ�ֱ�߽���ʽ����������߽���ʽΪ
���������ߺ�ֱ�߽���ʽ����������߽���ʽΪ![]() ��ֱ�߽���ʽ����ȥ
��ֱ�߽���ʽ����ȥ![]() ��
��![]() ������ֱ�������������У�ֻ��һ�����㣩������������ʽ�õ�����
������ֱ�������������У�ֻ��һ�����㣩������������ʽ�õ�����![]() �ķ�����������ȵ�ʵ����������
�ķ�����������ȵ�ʵ����������![]() �������
�������![]() ��ֵ��
��ֵ��
��3����Ϊ���κ���ͼ����ֱ�����У����Ѷ��κ�����ֱ�߽���ʽ�������õ�����![]() �ķ��������������ʵ����������
�ķ��������������ʵ����������![]() ��������ʽ��
��������ʽ��![]() ���ɿ���
���ɿ���![]() ����
����![]() �Ķ��κ�������Ӧ�����߿������ϣ��Գ���Ϊֱ��
�Ķ��κ�������Ӧ�����߿������ϣ��Գ���Ϊֱ��![]() ���������۶Գ�����
���������۶Գ�����![]() ��ࡢ�м䡢�Ҳ��������������ͼ�εã������Գ�����
��ࡢ�м䡢�Ҳ��������������ͼ�εã������Գ�����![]() ��༴
��༴![]() ʱ����ͼ���֪
ʱ����ͼ���֪![]() ʱ
ʱ![]() ��
��![]() ���������������
���������������![]() ʱ
ʱ![]() ȡ����Сֵ����
ȡ����Сֵ����![]() ��
��![]() ����õ�����
����õ�����![]() �ķ��̣������⣻�����Գ�����
�ķ��̣������⣻�����Գ�����![]() ��Χ��ʱ��
��Χ��ʱ��![]() ʱ��ȡ����Сֵ
ʱ��ȡ����Сֵ![]() ���÷���
���÷���![]() ����ã�
����ã�![]() �������Գ�����2���Ҳ༴
�������Գ�����2���Ҳ༴![]() ʱ����ͼ���֪
ʱ����ͼ���֪![]() ʱ
ʱ![]() ��
��![]() ���������������
���������С������![]() ʱ
ʱ![]() ȡ����Сֵ����
ȡ����Сֵ����![]() ��
��![]() ���뼴���
���뼴���![]() ��ֵ��
��ֵ��
�⣺��1����ͼ1������![]() ���ǹ���
���ǹ���![]() ��
��![]() ���߽�
���߽�![]() ���ڵ�
���ڵ�![]()
![]() ��
��![]()
![]() ��
��![]()
![]()
![]()
![]()
![]() ��
��![]()
![]()
![]()
![]()
![]()
![]()
![]()
��ֱ��![]() ����ʽΪ��
����ʽΪ��![]()
![]() ����ã�
����ã�![]()
![]() ����
����![]() ��
��![]() �����ߵĽ���ʽΪ
�����ߵĽ���ʽΪ![]() ;
;
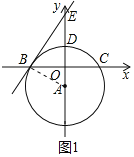
��2��![]() ������
������![]() ������
������![]()
![]() ����ã�
����ã�![]()
![]() �����߽���ʽ��
�����߽���ʽ��![]()
![]() ֱ��
ֱ��![]() ������
������![]()
![]() ���ɵã�
���ɵã�![]()
![]() ֱ�߽���ʽΪ��
ֱ�߽���ʽΪ��![]()
![]() ֱ��������������
ֱ��������������
![]() ����
����![]() �ķ���
�ķ���![]() ��������ȵ�ʵ����
��������ȵ�ʵ����
���������ã�![]()
![]() ��
��![]()
��ã�![]()
![]() ֱ�߽���ʽΪ
ֱ�߽���ʽΪ![]() ��
��
��3��![]() ����
����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ����
����
![]() ����
����![]() �ķ���
�ķ���![]() ��������ȵ�ʵ����
��������ȵ�ʵ����
���������ã�![]()
![]() ��
��![]()
�����ã�![]() ���ɿ���
���ɿ���![]() ����
����![]() �Ķ��κ�����
�Ķ��κ�����
��Ӧ�����߿������ϣ��Գ���Ϊֱ��![]()
![]() ��
��![]() ʱ��
ʱ��![]() ����СֵΪ
����СֵΪ![]()
����ͼ2����![]() ʱ����
ʱ����![]() ʱ
ʱ![]() ��
��![]() �����������
�����������
![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]()
![]() �������⣻
�������⣻

����ͼ3����![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]()
![]() ����ã�
����ã�![]() ��
��
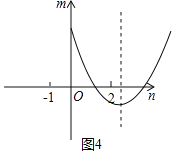
����ͼ4����![]() ʱ����
ʱ����![]() ʱ
ʱ![]() ��
��![]() ���������С
���������С
![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]()
![]() ����ã�
����ã�![]() ��
��![]() ����ȥ��
����ȥ��
����������![]() ��ֵΪ1��
��ֵΪ1��![]() ��
��

 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�