Question

【题目】在△ABC中，AB＝AC，BC＝8，D为边AC的中点.

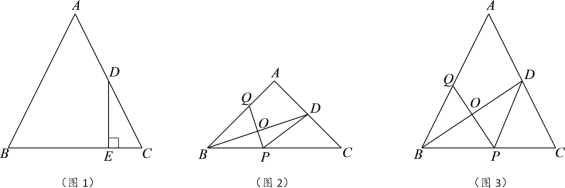
（1）如图1，过点D作DE⊥BC，垂足为点E，求线段CE的长；

（2）连接BD，作线段BD的垂直平分线分别交边BC、BD、AB于点P、O、Q．

①如图2，当∠BAC＝90°时，求BP的长；

②如图3，设tan∠ABC＝x，BP＝y，求y与x之间的函数表达式和tan∠ABC的最大值．

Answer 1

【答案】（1） ；（2）①；② ；tan∠ABC有最大值为

【解析】

（1）过点A作AH⊥BC交BC于点H，利用等腰三角形三线合一和平行线分线段成比例定理即可解决问题；

（2）①过点D作DH⊥BC交BC于点H，设，在 中利用勾股定理即可求解；

②过点D作DH⊥BC交BC于点H，同样在在 中利用勾股定理即可表示出y与x之间的函数表达式，再根据当y有最大值时，x也有最大值，即tan∠ABC有最大值即可求解.

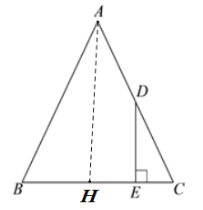
（1）如图，过点A作AH⊥BC交BC于点H

∵, BC＝8

∴

∵

∴

∵D为边AC的中点，

∴E为边CH的中点

∴

（2）①过点D作DH⊥BC交BC于点H

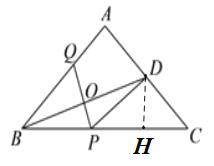
∵PQ垂直平分BD

∴BP=PD

∵∠BAC＝90°，AB＝AC

∴

∴

设，则，

在 中，

解得 ，即

②过点D作DH⊥BC交BC于点H

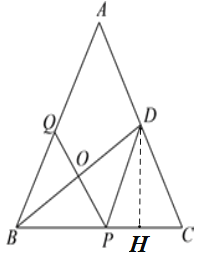
∵PQ垂直平分BD

∴BP=PD

∵，tan∠ABC＝tan∠ACB= x，BP＝y

∴

在 中，

∴

由得，

∴当y有最大值时，x也有最大值，即tan∠ABC有最大值.

∴当时，

解得 或（舍去）

∴tan∠ABC有最大值为