题目内容
【题目】已知抛物线![]() 的顶点为点
的顶点为点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出点![]() 的坐标为________;
的坐标为________;
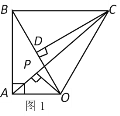
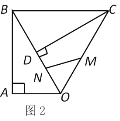
(2)如图,若![]() 、
、![]() 两点在原点的两侧,且
两点在原点的两侧,且![]() ,四边形
,四边形![]() 为正方形,其中顶点
为正方形,其中顶点![]() 、
、![]() 在
在![]() 轴上,
轴上,![]() 、
、![]() 位于抛物线上,求点
位于抛物线上,求点![]() 的坐标;
的坐标;
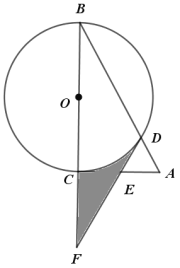
(3)若线段![]() ,点
,点![]() 为反比例函数
为反比例函数![]() 与抛物线
与抛物线![]() 在第一象限内的交点,设
在第一象限内的交点,设![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
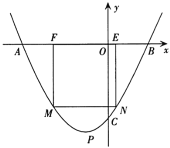
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)把函数变形为顶点式即可求解;
(2)设A(x1,0),B(x2,0),易得x1+x2=2,又OA=3OB得到x1=3x2,求出x1,x2,得到A,B坐标,将B(1,0)代入抛物线求出a,设E(m,0),则![]() ,EN=(m2+2m3),根据题意,得 2m+2=(m2+2m3),解得m的值即可求解;
,EN=(m2+2m3),根据题意,得 2m+2=(m2+2m3),解得m的值即可求解;
(3)由线段AB=2,得A(2,0),B(0,0),a=4,y=4x2+8x,当1<m<3时,对于抛物线y=4x2+8x,y随x的增大而增大,对于反比例函数![]() ,y随x的增大而减小,当x=1时,双曲线在抛物线上方,即
,y随x的增大而减小,当x=1时,双曲线在抛物线上方,即![]() >4×12+8×1,解得k>12,当x=3时,双曲线在抛物线下方,即
>4×12+8×1,解得k>12,当x=3时,双曲线在抛物线下方,即![]() <4×32+8×3,解得k<180,所以k的取值范围12<k<180.
<4×32+8×3,解得k<180,所以k的取值范围12<k<180.
(1)∵y=ax2+2ax+a4=a(x+1)24,
∴P(1,4);
故答案为:(1,4);
(2)设点![]() ,
,![]()
∵抛物线的对称轴为![]()
∴![]()
则![]()
又![]()
∴![]()
∴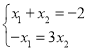
得![]() ,
,![]()
∴A(3,0),B(1,0),
把点![]() 代入
代入![]() 得
得![]()
解得![]()
∴![]()
设点![]() 坐标为
坐标为![]() ,F(n,0)
,F(n,0)
∴![]() ,∴n=-m-2
,∴n=-m-2
∴![]() ,
,![]()
根据题意得![]()
解得![]() ,
,![]() (舍去)
(舍去)
∴点![]() 的坐标为
的坐标为![]() ;
;
(3)∵![]() ,抛物线的对称轴为
,抛物线的对称轴为![]()
所以![]() ,
,![]() ,
,
把(0,0)代入得![]() ,
,
解之得,![]() ,
,
∴![]() ,
,
当![]() ,对于抛物线
,对于抛物线![]() 来说,
来说,![]() 随
随![]() 增大而增大;
增大而增大;
对于![]() ,
,![]() 随
随![]() 增大而减小,所以当
增大而减小,所以当![]() 时,双曲线在抛物线的上方,
时,双曲线在抛物线的上方,
即![]() ,解之得,
,解之得,![]()
当![]() 时,双曲线位于抛物线的下方,即
时,双曲线位于抛物线的下方,即![]() ,解之得,
,解之得,![]()
所以![]() 的取值范围为
的取值范围为![]() .
.