题目内容
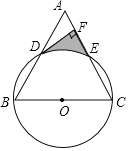
【题目】如图,在![]() 中,
中,![]() ,以直角边
,以直角边![]() 为直径的
为直径的![]() 交斜边
交斜边![]() 于点
于点![]() .点
.点![]() 为边
为边![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,
,
(1)求证:直线![]()
![]() 的切线;
的切线;
(2)若![]() ,求阴影部分的面积.
,求阴影部分的面积.
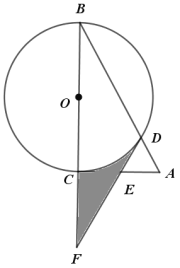
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)分别连结OD,OC,可证得![]() 是直角三角形,根据点
是直角三角形,根据点![]() 是斜边
是斜边![]() 的中点,得到
的中点,得到![]() ,由∠ECD+∠OCD=∠ACB=90°得∠EDC+∠ODC=∠ODE=90° ,从而证得直线
,由∠ECD+∠OCD=∠ACB=90°得∠EDC+∠ODC=∠ODE=90° ,从而证得直线![]()
![]() 的切线;
的切线;
(2)由(1)已证∠ODF=90°,根据∠B=30°,可得∠DOF=60°,得到∠F=30°,在![]() 中,可求得BC长,从而得到OD长,在
中,可求得BC长,从而得到OD长,在![]() 中,可求得DF长,所以阴影部分面积=△ODF的面积-扇形OCD的面积.
中,可求得DF长,所以阴影部分面积=△ODF的面积-扇形OCD的面积.
证明:(1)分别连结![]()
![]()
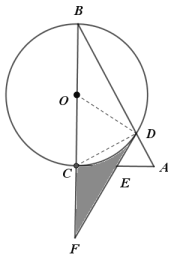
![]() ,
,
又![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]() 是直角三角形,
是直角三角形,
又![]() 点
点![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() ,
,
![]()
又![]()
![]() ,
,
直线![]() 是
是![]() 的切线.
的切线.
解:(2)由(1)已证:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,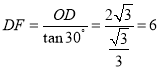
![]() 阴影部分的面积为:
阴影部分的面积为:![]()
![]()

练习册系列答案
相关题目