题目内容
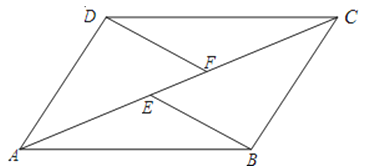
【题目】如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论,其中正确的有( )
①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ADE=![]() AB2 .
AB2 . 
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:∵四边形ABCD为菱形,
∴AD=AB,且∠A=60°,
∴△ABD为等边三角形,
又∵E、F分别是AB、AD的中点,
∴DE⊥AB,BF⊥AD,
∴∠GFA=∠GEA=90°,
∴∠BGD=∠FGE=360°﹣∠A﹣∠GFA﹣∠GEA=120°,
∴①正确;
∵四边形ABCD为菱形,
∴AB∥CD,AD∥BC,
∴∠CDG=∠CBG=90°,
在Rt△CDG和Rt△CBG中,![]() ,
,
∴Rt△CDG≌Rt△CBG(HL),
∴DG=BG,∠DCG=∠BCG=![]() ∠DCB=30°,
∠DCB=30°,
∴DG=BG=![]() CG,
CG,
∴DG+BG=CG,
∴②正确;
在Rt△BDF中,BD为斜边,在Rt△CGB中,CG为斜边,
且BD=BC,在Rt△CGB中,显然CG>BC,即CG>BD,
∴△BDF和△CGB不可能全等,
∴③不正确;
∵△ABD为等边三角形,
∴S△ABD=![]() AB2 ,
AB2 ,
∴S△ADE=![]() S△ABD=
S△ABD=![]() AB2 ,
AB2 ,
∴④不正确;
综上可知正确的只有两个,
故选B.
【考点精析】关于本题考查的菱形的性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目