题目内容
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
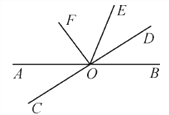
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
【答案】(1) OF⊥OD,理由见解析;(2) 60°.
【解析】试题分析:(1)根据角平分线的性质,可得![]() 与
与![]() 的关系,根据角的和差,可得
的关系,根据角的和差,可得![]() 的度数,可得答案;
的度数,可得答案;
(2)根据补角的性质, ![]() 可得
可得![]() 的度数,根据角的和差,可得
的度数,根据角的和差,可得![]() 的度数,根据角平分线的性质,可得答案.
的度数,根据角平分线的性质,可得答案.
试题解析:
(1)因为OF平分∠AOE,
所以∠AOF=∠EOF=![]() ∠AOE.
∠AOE.
又因为∠DOE=∠BOD=![]() ∠BOE,
∠BOE,
所以∠DOE+∠EOF=![]() (∠BOE+∠AOE)=
(∠BOE+∠AOE)= ![]() ×180°=90°,
×180°=90°,
即∠FOD=90°.
所以OF⊥OD.
(2)设∠AOC=x°,
因为∠AOC∶∠AOD=1∶5,
所以∠AOD=5x°.
因为∠AOC+∠AOD=180°,
所以x+5x=180,x=30.
所以∠DOE=∠BOD=∠AOC=30°.
又因为∠FOD=90°,
所以∠EOF=90°-30°=60°.

练习册系列答案
相关题目