��Ŀ����
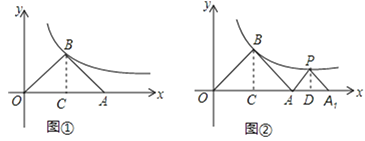
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������ABO�ĵױ�OA��x���ϣ�����B�ڷ���������y= ![]() ��x��0����ͼ���ϣ����ױ�OA�ϵĵ�A��x�������������������ƶ�ʱ������BҲ��֮�ڷ���������y=
��x��0����ͼ���ϣ����ױ�OA�ϵĵ�A��x�������������������ƶ�ʱ������BҲ��֮�ڷ���������y= ![]() ��x��0����ͼ���ϻ���������Oʼ��λ��ԭ�㣮
��x��0����ͼ���ϻ���������Oʼ��λ��ԭ�㣮


�� ��
��1����ͼ�٣�����A������Ϊ��6��0��ʱ�����B�����ꣻ
��2������A�ƶ���ʲôλ��ʱ��������ABO��ɵ���ֱ�������Σ���˵�����ɣ�
��3���ڣ�2���У���ͼ�ڣ���PA1A�ǵ���ֱ�������Σ���P�ڷ���������y= ![]() ��x��0����ͼ���ϣ�б��A1A����x���ϣ����A1������
��x��0����ͼ���ϣ�б��A1A����x���ϣ����A1������
���𰸡���1����3��4����2����A�ƶ�����![]() ��0��ʱ����ABO��ɵ���ֱ�������Σ�3����
��0��ʱ����ABO��ɵ���ֱ�������Σ�3����![]() ��0��
��0��
�������������������1������B��BC��x���ڵ�C���ɵ��������ε����ߺ�һ���ɵ�OC=AC=3��Ȼ���ɶ���B�ڷ���������y= ![]() ��x��0����ͼ���ϣ�������õ�B�����ꣻ��2����A�ƶ�����
��x��0����ͼ���ϣ�������õ�B�����ꣻ��2����A�ƶ�����![]() ��0��ʱ����ABO��ɵ���ֱ�������Σ�����B��BC��x���ڵ�C���ɵ���ֱ�������ε����ʣ��ɵ�OC=BC�����B��a��a����Ȼ���ɶ���B�ڷ���������y=
��0��ʱ����ABO��ɵ���ֱ�������Σ�����B��BC��x���ڵ�C���ɵ���ֱ�������ε����ʣ��ɵ�OC=BC�����B��a��a����Ȼ���ɶ���B�ڷ���������y= ![]() ��x��0����ͼ���ϣ���õ�B�����꣬�̶���õ�A�����ꣻ��3�����ȹ���P��PD��x���ڵ�D����AD=PD�������AD=b�����P��4
��x��0����ͼ���ϣ���õ�B�����꣬�̶���õ�A�����ꣻ��3�����ȹ���P��PD��x���ڵ�D����AD=PD�������AD=b�����P��4![]() +b��b�������ɵ�P�ڷ���������y=
+b��b�������ɵ�P�ڷ���������y= ![]() ��x��0����ͼ���ϣ����b��ֵ���̶���ô𰸣�
��x��0����ͼ���ϣ����b��ֵ���̶���ô𰸣�
���������
��1������B��BC��OA��C����OC=![]() OA=3��
OA=3��
��B�������3����x=3����y=![]()
�ã�y=4��
��B�������ǣ�3��4����
��2����A�ƶ�����![]() ��0��ʱ����ABO��ɵ���ֱ�������Σ�
��0��ʱ����ABO��ɵ���ֱ�������Σ�
���ɣ���ͼ�ڣ�����B��BC��x���ڵ�C��
�ߡ�AOB�ǵ���ֱ�������Σ�
��BC=OC= ![]() ,
,
���B��a��a����
�߶���B�ڷ���������y= ![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��a= ![]() ��
��
��ã�a=��![]() ����ֵ��ȥ����
����ֵ��ȥ����
��OC=![]() ��
��
��OA=2OC=![]() ��
��
���A�ƶ�����![]() ��0��ʱ����ABO��ɵ���ֱ�������Σ�
��0��ʱ����ABO��ɵ���ֱ�������Σ�
��3����ͼ�ڣ�����P��PD��x���ڵ�D��
�ߡ�PA1A�ǵ���ֱ�������Σ�
��PD=AD��
��AD=b�����P ![]()
�ߵ�P�ڷ���������![]()
��x��0����ͼ���ϣ�![]()
��ã�![]() (������ȥ)
(������ȥ)
��![]()
��OA1=OA+AA1= ![]()
���A1�������ǣ�![]() ��0��
��0��