题目内容
【题目】如图，一单杆高2.2m，两立柱之间的距离为1.6m，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状．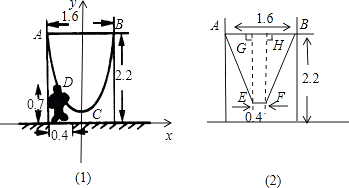 
（1）一身高0.7m的小孩站在离立柱0.4m处，其头部刚好触上绳子，求绳子最低点到地面的距离；
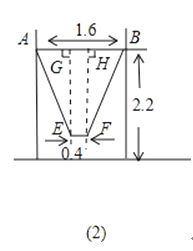
（2）为供孩子们打秋千，把绳子剪断后，中间系上一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳子正好各为2米，木板与地面平行，求这时木板到地面的距离．（供选用数据： 
≈1.8， 
≈1.9， 
≈2.1）
【答案】
（1）解：如图，建立直角坐标系，设二次函数为：y=ax2+c
∵D（﹣0.4，0.7），B（0.8，2.2）
∴ 
∴ 
∴绳子最低点到地面的距离为0.2米
（2）解：分别作EG⊥AB于G，E、FH⊥AB于H，
AG= 
（AB﹣EF）= （1.6﹣0.4）=0.6
在Rt△AGE中，AE=2，EG= 
≈1.9
∴2.2﹣1.9=0.3（米）
∴木板到地面的距离约为0.3米
【解析】（1）设二次函数为y=ax2+c，利用待定系数法求出a，c的值然后可求出绳子最低点到地面的距离．（2）本题要靠辅助线的帮助求出AG的值．然后根据勾股定理求出EG的值．
练习册系列答案
全能练考卷系列答案
相关题目
