Question

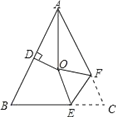
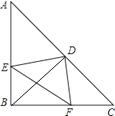
【题目】如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边中点，过D点作DE⊥DF，交AB于E，交BC于F,连接BD.

(1)求证：△CDF≌△BED

(2)若AE=4，FC=3，求AB长

Answer 1

【答案】（1）证明见解析；（2）7.

【解析】

（1）由“∠ABC=90°，DE⊥DF”可以求出∠BDE=∠FDC，由等腰直角三角形，D为AC边的中点，可得∠ABD=∠C，BD=DC，从而证得全等；（2）由△CDF≌△BED，可知BE=FC，从而求出AB的长

（1）证明：∵三角形ABC是等腰直角三角形，D为AC边的中点，

∴BD=DC, ∠ABD=∠C=45°，BD⊥AC，

∴∠BDF+∠FDC=90°，

又∵DE⊥DF

∴∠BDF+∠BDE=90°，

∴∠FDC=∠BDE.

∴△BED≌△CFD

（2）∵△BED≌△CFD∴BE=FC=3,又AE=4，所以AB=AE+BE=7